A spherical planet has uniform density π2×104kg/m3. Find out the minimum period for a satellite in a circular orbit around it in seconds (Use G=203×10−11N−m2kg2).
The correct Answer is:C
Time period is minimum for the satellites with minimum radius of the orbit i.e., equal to the radius of the planet. Therefore,
GMmR2=mv2R⇒v=√GMR
Tmin=2πR√GMR=2πR√R√GM Using M=43πR3ρTmin=√3πGρ
Using values Tmin = 3000 s ∴ P = 300
Similar Questions
A satellite revolves around a planet of mean density 4.38×103kg/m3, in an orbit close to its surface. Calculate the time period of the satellite.
Take, G=6.67×10−11Nm2kg−2.
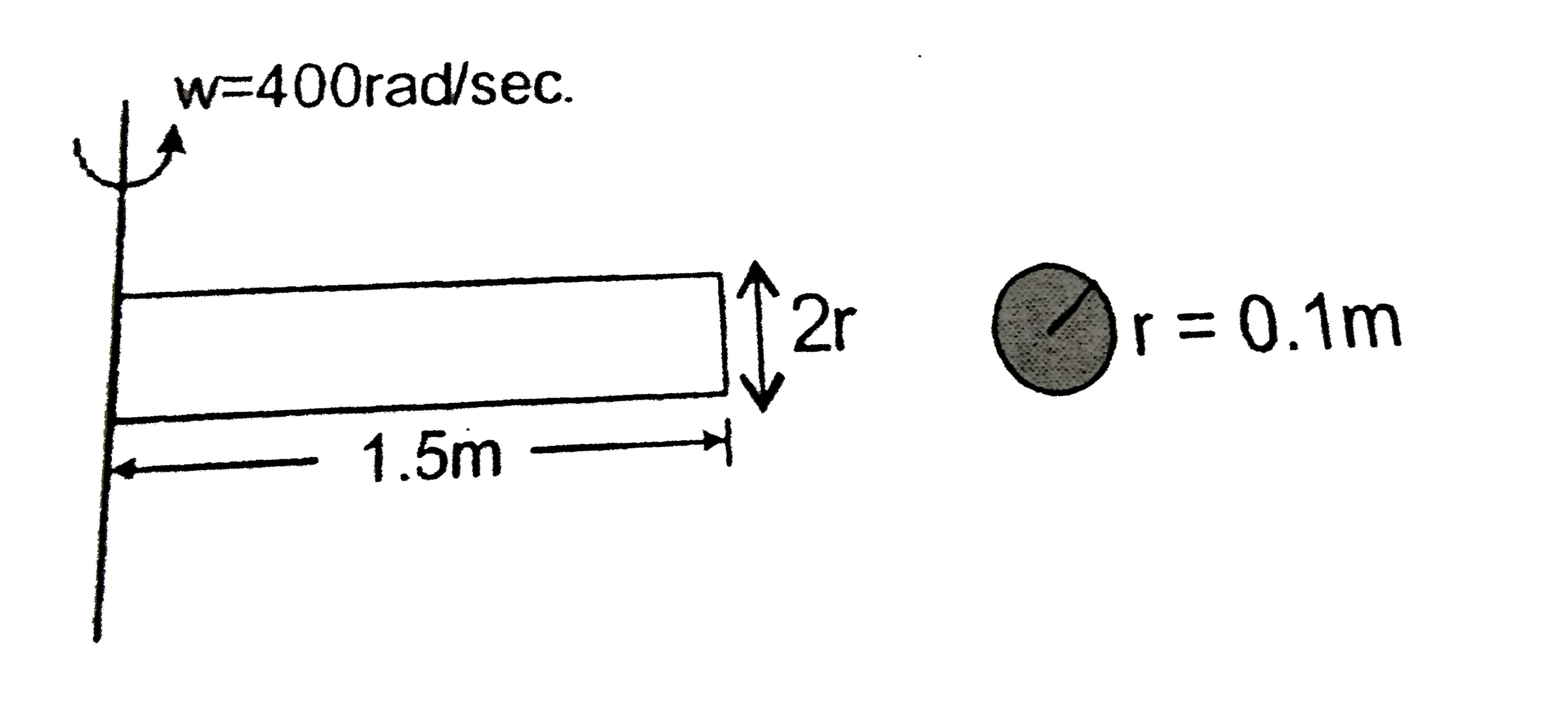
View SolutionA rod of 1.5m length and uniform density 104kg/m3 is rotating at an angular velocity 400rad/sec about its one end in a horizontal plane. Find out elongation in rod.
Given y=2×1011N/m2
View Solution
Knowledge Check
Two metal spheres are falling through a liquid of density 2×103kg/m3 with the same uniform speed. The material density of sphere 1 and sphere 2 are 8×103kg/m3 and 11×103kg/m3 respectively. The ratio of their radii is :-
A118B√118C32D√32_S01_033_Q01.png)
A triple star system consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The mass m of the outer stars is:A118×1030B1516×1030C403×1030D203×1030The planet Mars has two moons, if one of them has a period 7 hours, 30 minutes and an orbital radius of 9.0×103 km. Find the mass of Mars.
{Given 4π2G=6×1011N−1m−2kg2}A5.96×1019 kgB3.25×1021 kgC7.02×1025 kgD6.00×1023 kg
A satellite revolves in an orbit close to the surface of a planet of mean density 5.51×103kgm−3. Calculate the time period of satellite.
Given G=6.67×10−11Nm2kg−2.
View SolutionA uniform solid sphere has radius 0.2 m and density 8×103kg/m2. Fing the moment of inertia about the tangent to its surface. (π=3.142)
View SolutionThe mass of planet Jupiter is 1.9×107kg and that of the Sun is 1.9x1030kg. The mean distance of Jupiter from the Sun is 7.8×1011m. Calculate te gravitational force which Sun exerts on Jupiter. Assuming that Jupiter moves in circular orbit around the Sun, also calculate the speed of Jupiter G=6.67×10−11Nm2kg−2.
View SolutionGiven Y=2×1011N/m2,ρ=104kg/m3
Find out elongation in rod.

View SolutionYoungs modulus of a string of length 1m and Density 900Kgm3 is 9×109Nm2. Find the minimum reasonance frequency in (Hz) can be produced in the string if strain in the string is 4.9×10−4.
View Solution