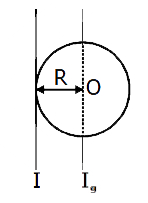
A uniform solid sphere has radius 0.2 m and density $8 \times 10^{3} k g / m^{2}$ . Fing the moment of inertia about the tangent to its surface. $(π = 3.142)$

Video Solution

Text Solution

Verified by Experts

We have, redius (R) =0.2 m and density $(p) = 8 \times 10^{3} k g / m^{2}$
Moment of inertia about the tangent to its surface,
$I = I_{C} + M R^{2}$
[ using parallel axis theorem]
$\frac{2}{5} M R^{2} + M R^{2}$
$= \frac{7}{5} M R^{2} ... ... (i)$
But, Mass (M) =Volume (V) $\times$ Density (p)
$M = V_{p} = (\frac{4}{3} π R^{3}) p$
Putting the value of M ing (i), we get
$I = \frac{7}{5} (\frac{4}{3} π R^{3}) p R^{2}$
$= \frac{28}{15} π R^{5} p$
$= \frac{28}{15} \times 3.142 \times {(2 \times 10^{- 1})}^{5} \times 8000$

Updated on:21/07/2023

A sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the sphere is
A $5 k g m^{2}$
B $2.7 k g m^{2}$
C $3.5 k g m^{2}$
D $4.5 k g m^{2}$
A sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the sphere is
A5 kg $m^{2}$
B $2.7$ kg $m^{2}$
C3.5 kg $m^{2}$
D4.5 kg $m^{2}$
If moment of inertia of a solid sphere of mass 5kg about its diameter is $50 k g m^{2}$ . Its moment of inertia about its tangent in kg $m^{2}$ is
A260
B250
C240
D175