A planet of mass m is the elliptical orbit about the sun (m<<Msun) with an orbital period T. If A be the area of orbit, then its angular momentum would be:
2mAT
mAT
mA2T
2mAT
The correct Answer is:A
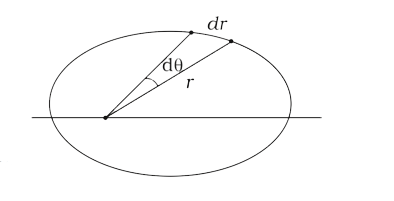
Area of the triangle shown is dA=12r×dr
⇒dA=12×r×rdθ=r22dθ
Dividing both side by dt ,
dAdt=r22dθdt=r22ω=mr2ω2m=Iω2m=L2m⇒dA=L2mdt
Integrating both sides, we get ⇒A=L2m×T⇒L=2mAT
Similar Questions
A planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
View SolutionA planet of mass m is revolving round the sun (of mass Ms) in an elliptical orbit. If →v is the velocity of the planet when its position vector from the sun is →r, then areal velocity of the positon vector of the planet is :
View Solution
Knowledge Check
A planet of mass m is in an elliptical orbit about the sun with an orbital period T. If A be the area of orbit, then its angular momentum would be
A2mATBmATCmA2TD2mATA planet of mass m is moving around the sun in an elliptical orbit of semi-major axis a :
AThe total mechanical energy of the planet is varying periodically with timeBThe total energ of the planet is constant and equals −GmMs2a,Ns is mass of sunCTotal mechanical energy of the planet is constant and equals −GmMsa,M2 is mass of sunDDate is insufficient of arrice at a conclusionA planet of mass m is moving in an elliptical orbit about the sun (mass of sun = M). The maximum and minimum distances of the planet from the sun are r1 and r2 respectively. The period of revolution of the planet wil be proportional to :
Ar3/21Br3/22C(r1−r2)3/2D(r1+r2)3/2
A planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionThe areal velocity of a planet of mass m moving in elliptical orbit around the sun with an angular momentum of L units is equal to
View Solution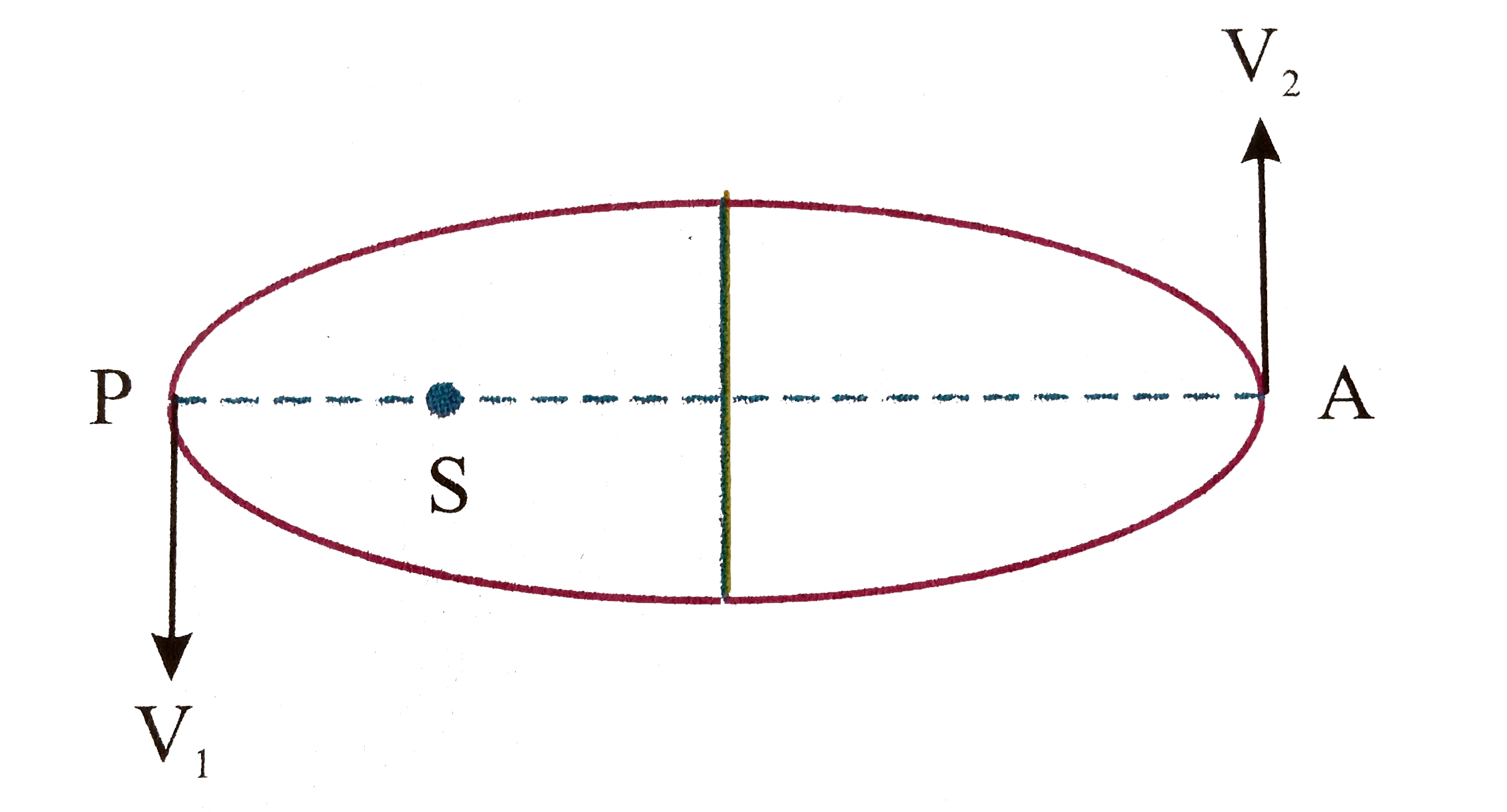
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find total energy of planet interms of given parameters.
View SolutionA planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at

View SolutionA planet of mass M is revolving round the sun in an elliptical orbit. If its angular momentum is J then the area swept per second by the line joining planet to sun will be :-
View Solution
