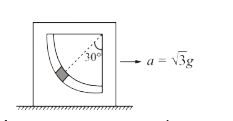
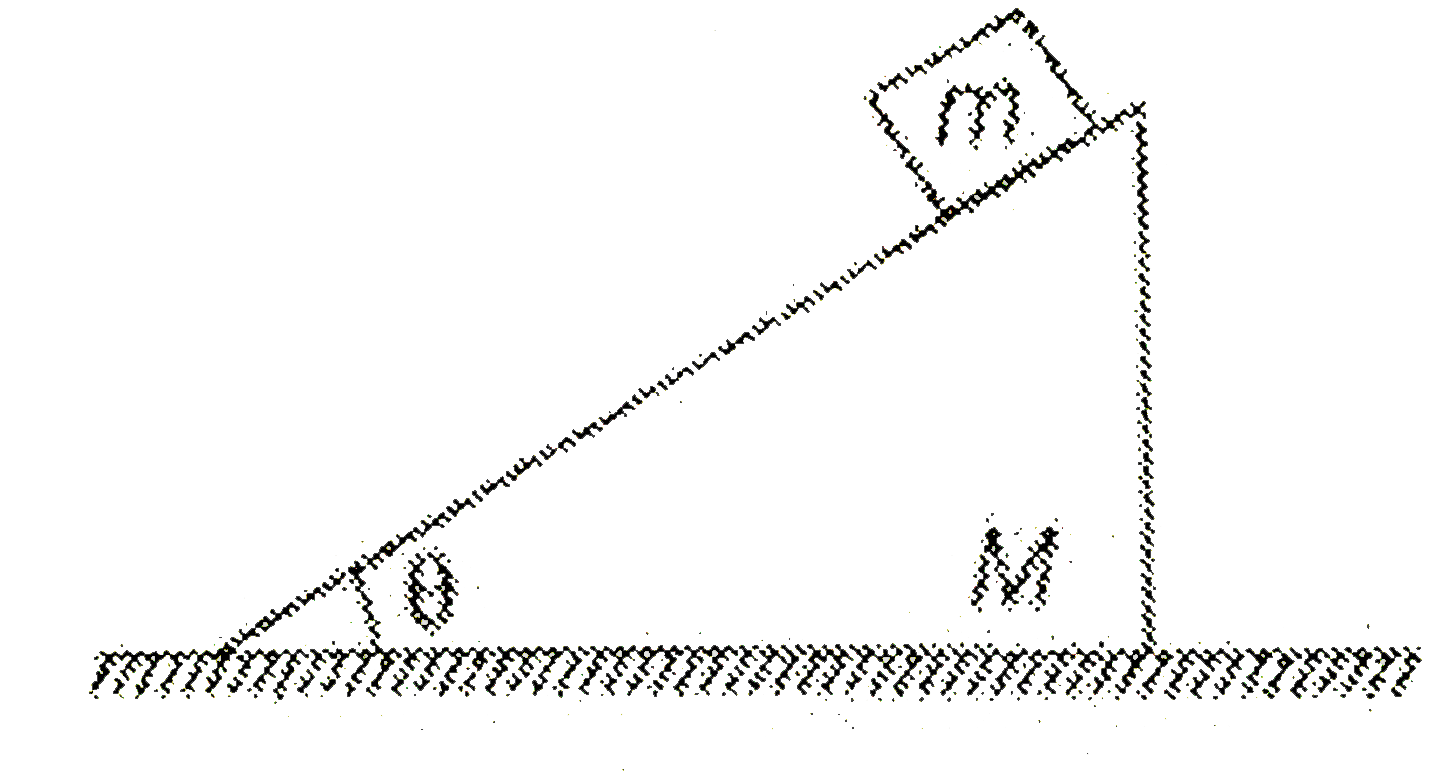
A wedge with a rough groove in the shape of a quarter of a circle is kept on a smooth table (see figure). A small block is placed in the groove with a small clearance. The wedge is moved with an acceleration√3g . If the block is to remain stationary relative to groove in the position shown, the coefficient of friction required can be:
13
14
15
910
The correct Answer is:D
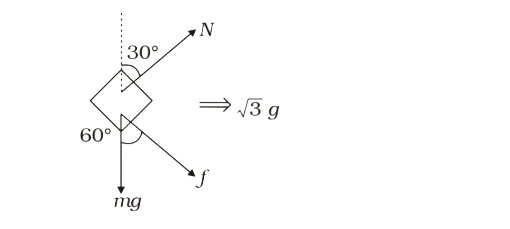
Ncos30∘=mg+fcos60∘
Nsin30∘+fsin60∘=mg√3
Put f=μN and solve to get μ=1√3
This means mi≥1√3.
Similar Questions
A block of mass m is placed on the rough incline of a wedge of mass M and inclination α to the horizontal. Calculate the maximum and minimum acceleration that can be imparted to the wedge so that the block may remain stationary relative to the wedge. The coefficient iof friction between the block and the wedge is μ.
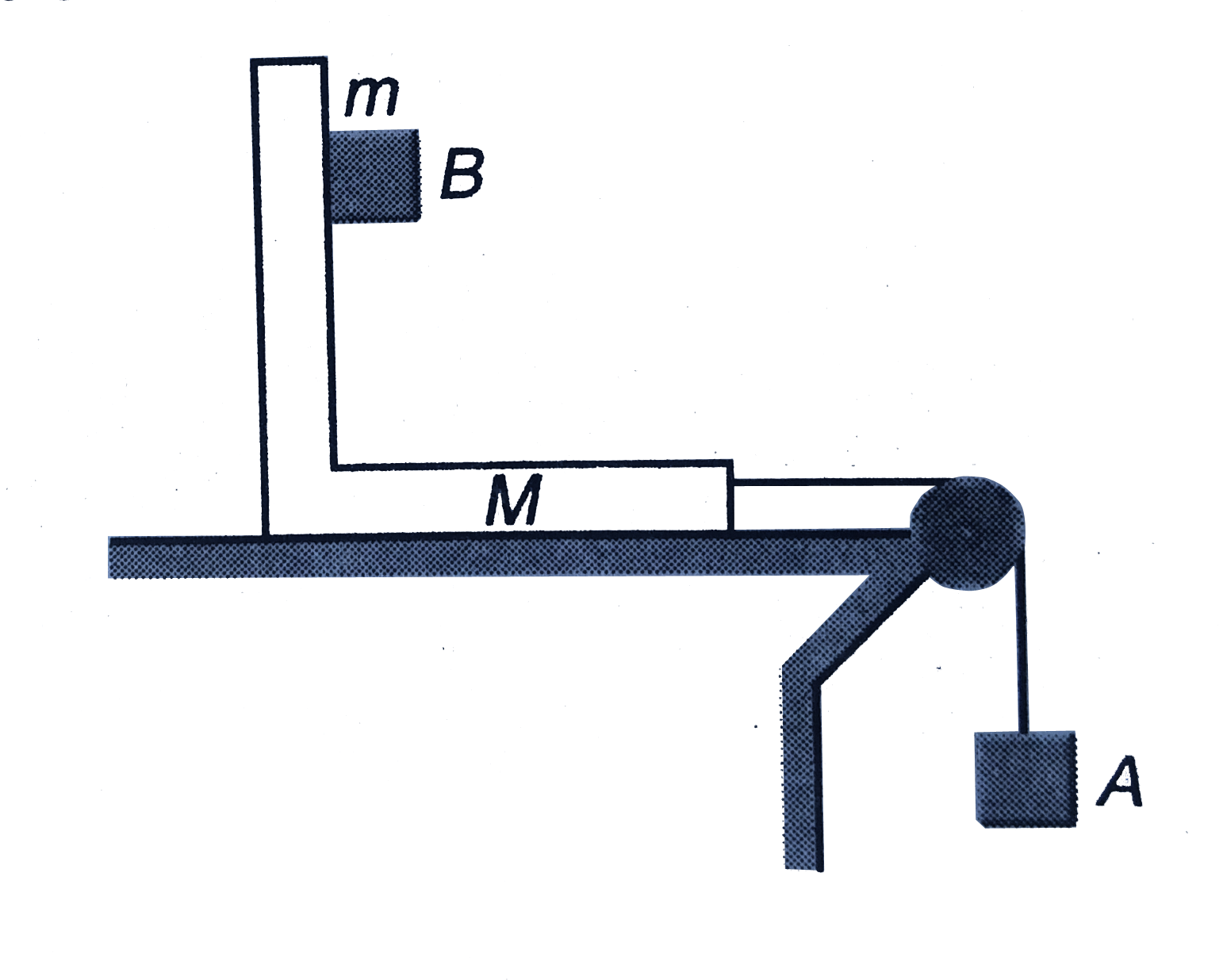
View SolutionThe figure an L shaped body of mass M placed on smooth horizontal surface. The block A is connected to the body by means of an inexiensible string , which is passing over a smooth pulley of negligible mass.Another block B of mass m is placed against a vertical wall of the body. Find the minimum value of the mass of block A so that B remain stationary relative to the wall. Coefficient of friction between the block B and the vertical wall is μ.
View Solution
Knowledge Check
A block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
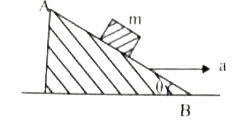 Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ
Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθA block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.
 Aa=gtanθBa=gcosecθCa=cosθDa=gsinθ
Aa=gtanθBa=gcosecθCa=cosθDa=gsinθAs shown in the figure a block of mass 'm' is placed on a smooth wedge moving with constant acceleration such that block does not move with respect to the wedge. Find work done by the net force on the block in time t. (Initial speed is 0)
 Am(gttanθ)2Bm3(gttanθ)2C49m(gttanθ)2Dm2(gttanθ)2
Am(gttanθ)2Bm3(gttanθ)2C49m(gttanθ)2Dm2(gttanθ)2
A small block of mass m is kept on a rough inclined surface of inclination θ fixed in a car. The car moves with a uniform velocity v and the block does not slide on the wedge. The work done by the force of friction on the block in time t will be
_PHY_E05_201_Q06.png)
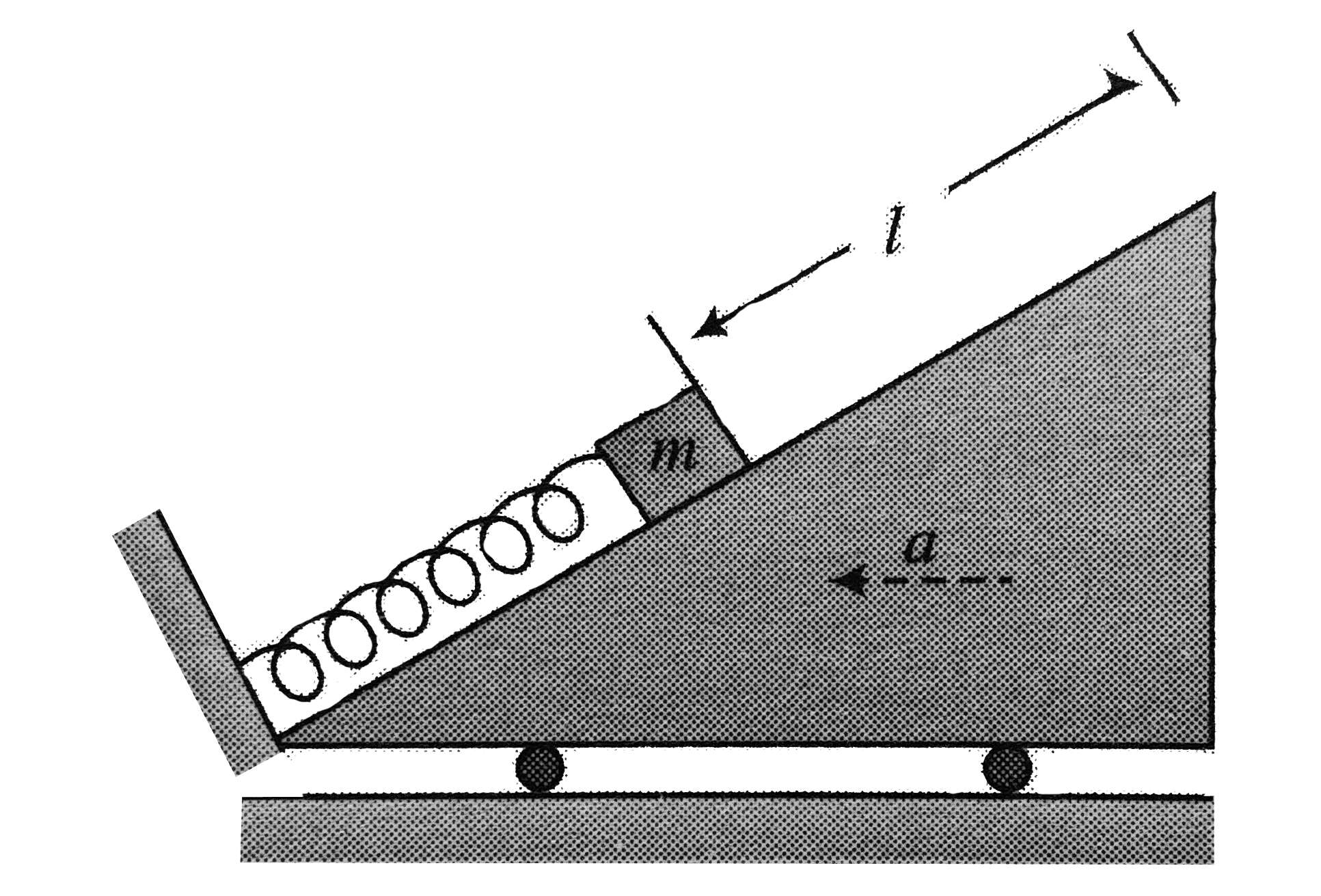
View SolutionA block of mass m is welded with a light spring of stiffness k. The spring is initially relaxed. When the wedge fitted moves with an acceleration a, as shown in figure. 8.60, the block slides through a maximum distance l relative to the wedge. If the coefficient of kinetic friction between the block and the wedges is μ, find the maximum deformation l of the spirng by using work-energy theorem.
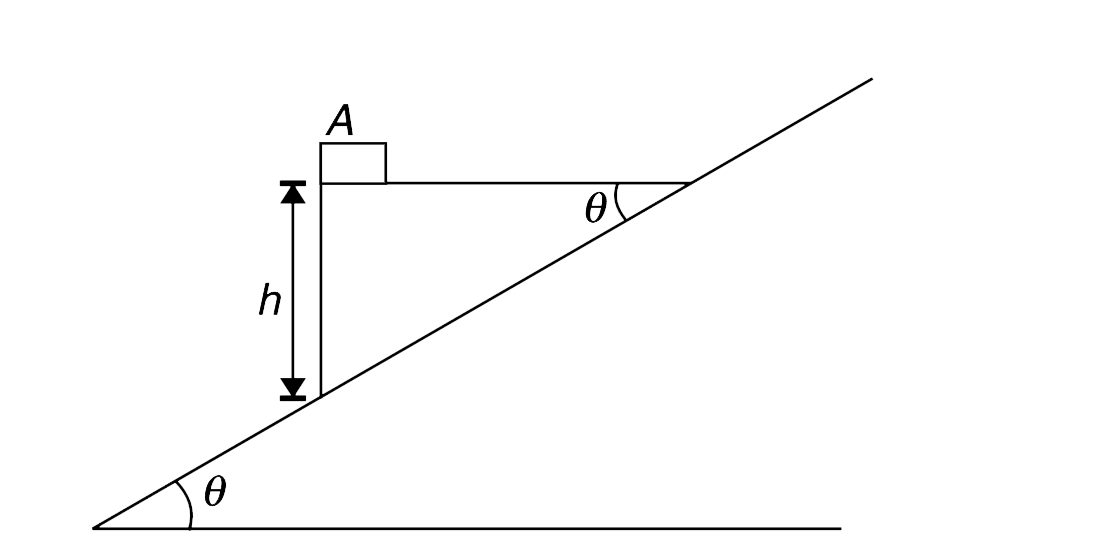
View SolutionA wedge is placed on the smooth surface of a fixed incline having inclination θ with the horizontal. The vertical wall of the wedge has height h and there is a small block A on the edge of the horizontal surface of the wedge. Mass of the wedge and the small block are M and m respectively.
(a) Find the acceleration of the wedge if friction between block A and the wedge is large enough to prevent slipping between the two.
(b) Find friction force between the block and the wedge in the above case. Also find the normal force between the two.
(c) Assuming there is no friction between the block and the wedge, calculate the time in which the block will hit the incline.
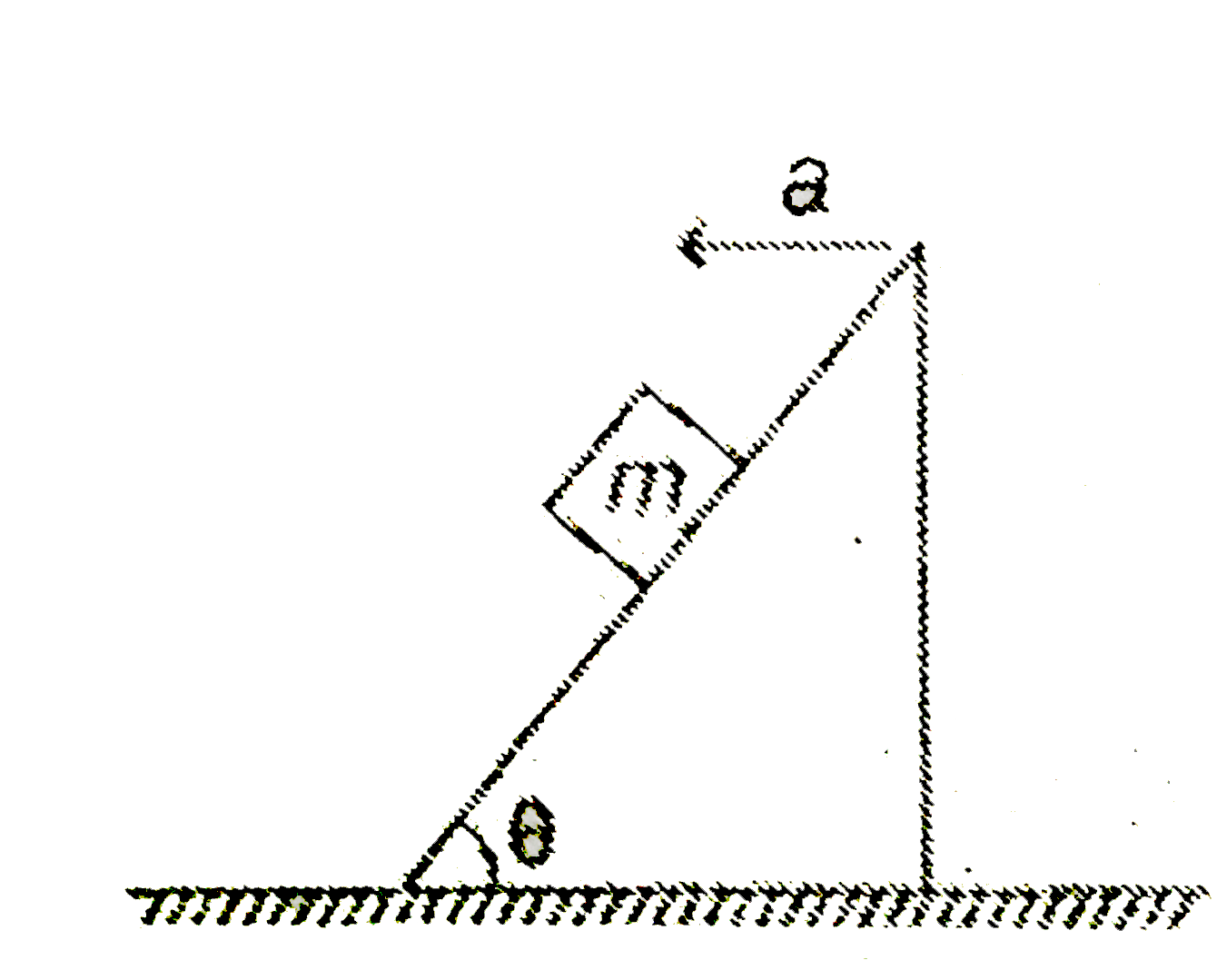
View SolutionA triangular wedge is placed on smooth horizontal surface. A block is placed on wedge as shown in the figure. Coefficient of friction between block and wedge is μ. Initially system reamins at rest.
View SolutionA small block of mass m is released from a fixed smooth wedge in figure. Initial point is marked as A. Bottom of wedge is marked as B and at a point C the block stops because the straight part of floor is rough.

The friction coefficient of the block with the floor is :
View Solution