A block of mass m is welded with a light spring of stiffness k. The spring is initially relaxed. When the wedge fitted moves with an acceleration a, as shown in figure. 8.60, the block slides through a maximum distance l relative to the wedge. If the coefficient of kinetic friction between the block and the wedges is μ, find the maximum deformation l of the spirng by using work-energy theorem.
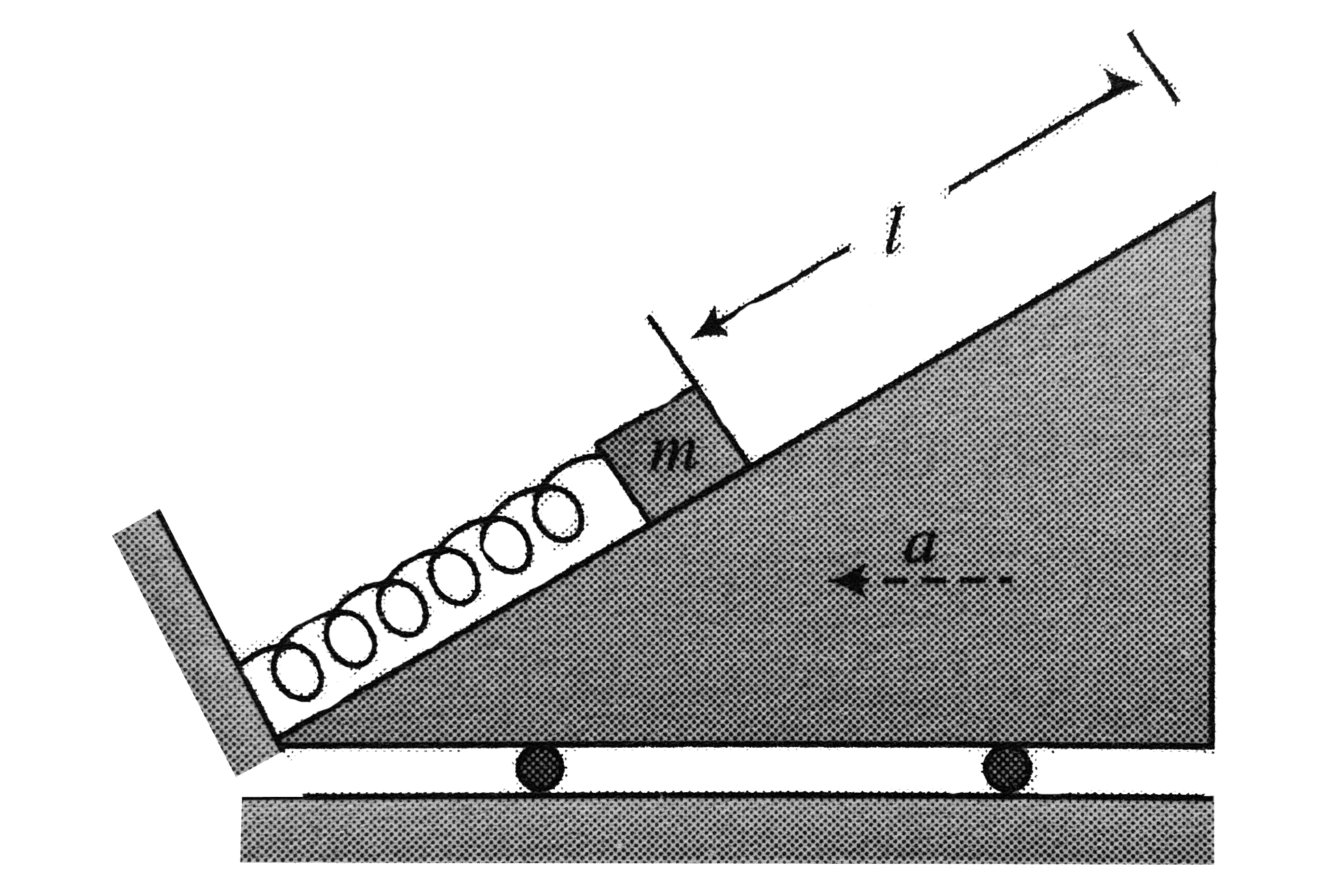
In this case, we are given the block slides through a distance l relative to the wedge. We can apply work-energy theorem from the frame of reference of wedge.
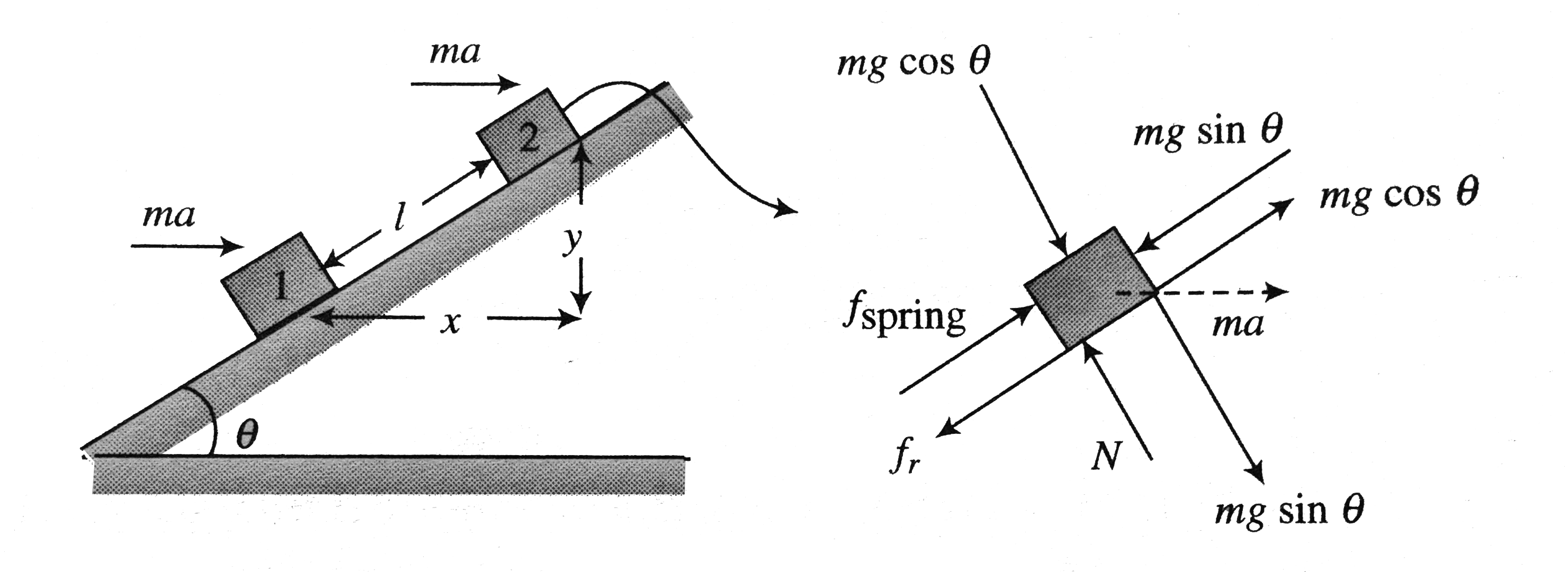
While the block is displaced from point 1 to point 2, work done by all the forces are given as follows:
Work: Wgr=−mglsinθ, Wsp=−Kl22
Wf=(μN)⋅l
N=mgcosθ+masinθ
Wf=−μmglcosθ−μmasinθ
and Wpseudo=(macosθ)l=malcosθ
W-E theorem: Summing upall workds, the total done is
Wtotal=Wgr+Wsp+Wf+Wpseudo
W=−mglsinθ1−μmglcosθ3+malcosθ4−12kl22+Fl−μmalsinθ3
Since the block was at rest at 1 and will remain at rest relative to the wedge, we can write ΔK=0 (relative to the wedge). Using work-energy theorem relative to the wedge, we have W=ΔK=0.
Substituting W=0, we have
−mg/sinθ−12kl2−μmgcosθ−μmalsinθ+malcosθ=0
l=2k[ma(cosθ−μsinθ)−mg(sinθ+μcosθ)]
=2mk[a(cosθ−μsinθ)−g(sinθ+μcosθ)]
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
The coefficient of friction between the block and the wedge is μ. Friction between the wedge and the table is to be neglected.
View SolutionA block of mass m is placed on the rough incline of a wedge of mass M and inclination α to the horizontal. Calculate the maximum and minimum acceleration that can be imparted to the wedge so that the block may remain stationary relative to the wedge. The coefficient iof friction between the block and the wedge is μ.
View Solution
Knowledge Check
A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2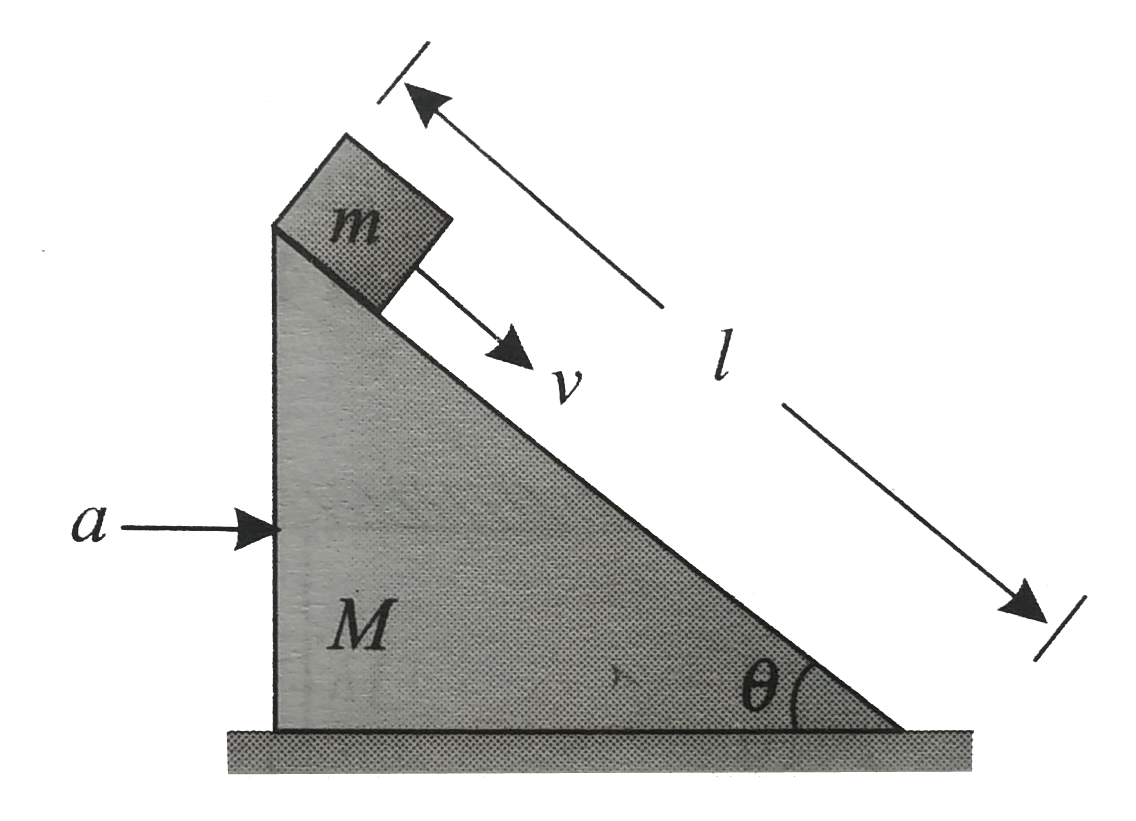
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
Q. The normal reaction between wedge and block is:AmgcosθBmgsecθCmgcotθDm>anθFigure shows an irregular wedge of mass m placed on a smooth horizontal surface. Part BC is rough.
If the coefficient of friction between the block and wedge is μ, and the block comes to rest with respect to wedge at a point E on the rough surface then BE will beAHμBH−hμChμDnone of these
The coefficient of friction between the wedge and the table is μ. Friction between the block and the wedge is to be neglected.
View SolutionA block of mass m is connected with a rigid wall by light spring of stiffness k. Initially the spring is relaxed.

If the block is pushed with a velocity v0, it oscillates back and forth and stops. Assuming μ as the coefficient of kinetic friction between block and ground, find the work done by friction till the block stops.
View SolutionA block lies on a wedge with the slope angle α. The coefficient of static friction between the bar and the wedge is μ<tanα. What should be the acceleration of the wedge to prevent the bar from sliding down?
View SolutionTwo blocks of Masses M and 2M are connected by a spring of stiffness k .The coefficient of friction between the blocks and the surface is mu Find the minimum constant force F to be applied to 2m in order to slide the mass M .
View SolutionTwo blocks of mass m and 2m are arranged on a wedge that is fixedd on a horizontal surface. Friction coefficient between the block and wedge are shown . Find the magnitude of acceleration of two blocks.

View Solution
