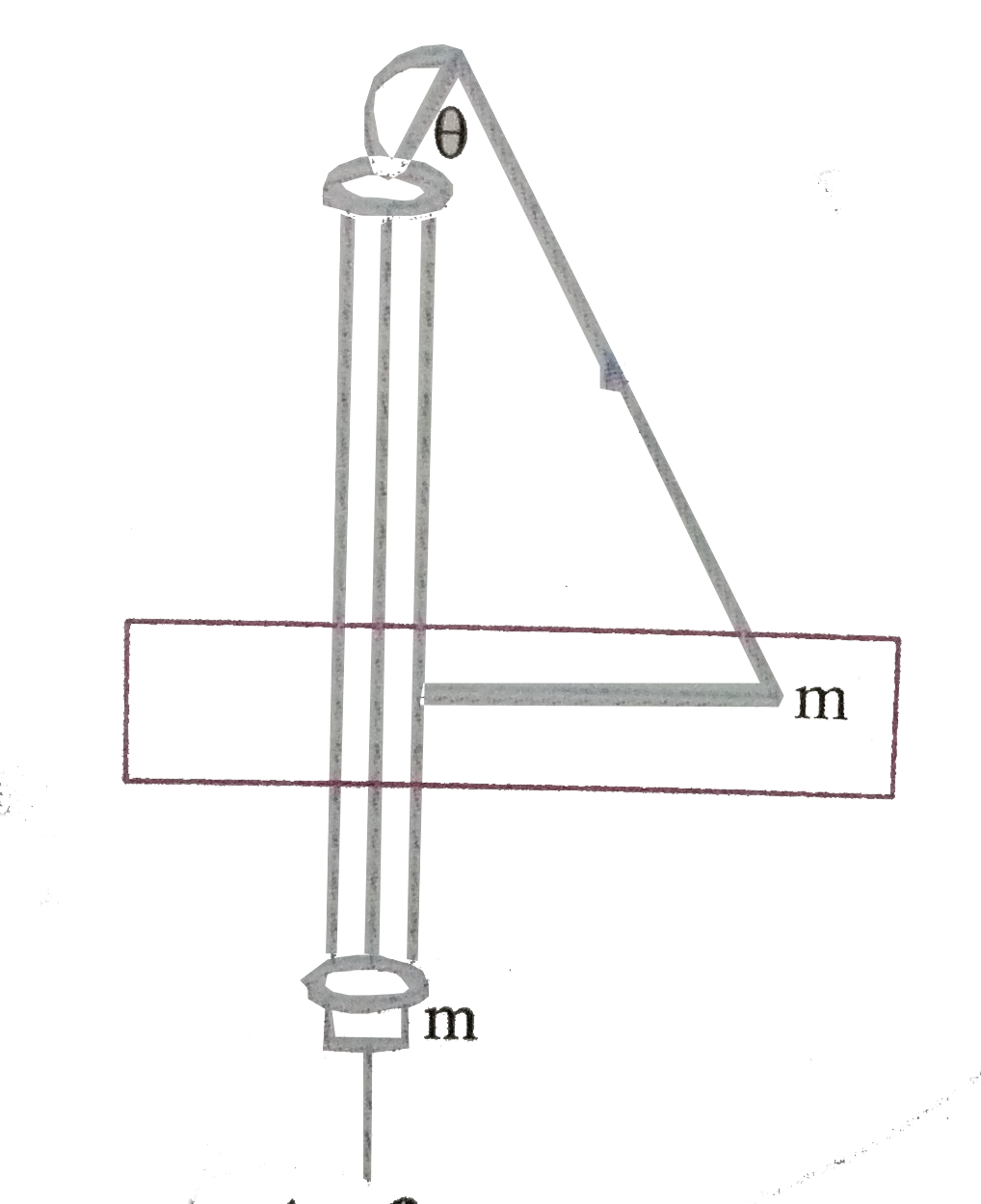
A large mass M and a small mass m hang at the two ends of string that passes through a smooth tube as shown in fig. The mass m moves around in a circular path which lies in a horizantal plane. The length of the string from the mass m to the top of the tube is of length l and θ is the angle this length makes with the vertical, what should be the frequency of rotation of the mass m so that M remains stationary if M=16kg,m=4kg,l=1m and g=π2m/s2
32π√MgmL
2π√mLMg
12π√MgmL
12π√Lg
The correct Answer is:C
T = mb (1) For hanging mass
Tsinθ=m(Lsinθ)ω2 (2) for m
From (1) and (2)
ω2=mgmLf=12π√MgmL
Similar Questions
A large mass M and a small mass m hang at two ends of a string that passes over a smooth tube as shown in the figure. The mass m moves around a circular path which lies in a horizontal plane. The length of string from the mass m to the top of the tube is l and θ is the 'angle' this length makes with the vertical. What should be the frequency of rotation of mass m, so that the mass M remains stationary?

View SolutionA large mass M and a small mass m hang at the two ends of string passing through a smooth tube. The mass m moves around in a circular path in a horizontal plane. The length of the string from the mass m to the top of the tube of the tube is l and θ is the angle this length makes with the vertical. What should be the frequency of rotation of the mass m so that M remains stationary ?
View Solution
Knowledge Check
A sphere of mass m is tied to end of a string of length l and rotated through the other end along a horizontal circular path with speed v . The work done in full horizontal circle is
A0B(mv2l).2πlCmg.2πlD(mv2l).(l)A particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√TmlThe linear mass density 'μ' of the string is (where, mass of the string = m, length of the string = L)
AmLBmLCmt2DmL3
A simple pendulum is hanging from the roof of a trolley which is moving horizontally with acceleration g. If length of the string is L and mass of the bob is m, then time period of oscillation is
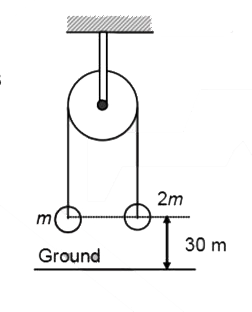
View SolutionTwo masses m and 2m are connected by a massless string, which passes over a pulley as shown in figure. The masses are held initially with equal lengths of the strings on either side of the pulley. Find the velocity of masses at the instant the lighter mass moves up a distance of 15m. ( g=10m/s2 )
View SolutionThe linear mass density μ of the string is (where, mass of the string = m, length, of the string g = L)
View SolutionA pendulum consists of a small mass m at the end of a string of length L. The pendulum is pulled aside making an angle θ with the vertical and released. Taking the suspension point as the axis, at the instant of release
View SolutionA simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle θ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
View Solution
