A 70kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3m rotating about its verticle axis. The coefficient of friction between the wall and his clothing is 0.15 . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
4.7 rad/s
9.8 rad/s
24 rad/s
1 rad/s
The correct Answer is:A
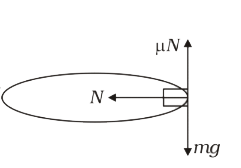
N=mRω2
μN=mg
From these two equations we get
ω=√gμR
=√9.80.15×3=4.7 rad/s
Similar Questions
A 90 kg man is standing in contact with the wall of a cylindrical drum of radius 2 m. The drum is rotating about its vertical axis with an angular speed of 100 rpm. Calculate the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall when the floor is suddenly removed. The coefficient of friction between wall and clothing is 0.1.
View SolutionA person stands in contact against the inner wall of a rotor of radius r. The coefficient of friction between the wall and the clothing is μ and the rotor is rotating about vertical axis. The minimum angular speed of the rotor so that the person does not slip downward is
View Solution
Knowledge Check
A person stands in contact against the inner surface of a cylindrical drum of radius (R ) rotating with angular velocity ω . The coefficient of friction between the inner surface of the minumum rotational speed of the cylinder , which enables the person to ramain stuck to the wall , when the platform on which the person was standing is suddenly removed ?
A√μRgB√gμRC√2gμRD√rgμA person stands in contact against a wall of cylindrical drum of radius 'r' rotating with an angular velocity ω. If μ is coefficient ofn static fiction between the wall and the person , then the minimum rotational speed which enables the person to remain struck to the wall will be
A√gμrB√μrgC√2gμrD√grμA block of mass 10 kg in contact against the inner wall of a hollow cylindrical drum of radius 1m. The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be (g=10m/s2)
A10πrad/sB√10rad/sC102πrad/sD10rad/s
A block of mass 10 kg is in contact against the inner wall of a hollow cylindrical drum of radius 1 m. The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be (g=10m/s2)
View SolutionA block of mass 10 kg in contact against the inner wall of a hollow cylindrical drum of radius 1m. The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be (g=10m/s2)
View SolutionIn a 'well of death' a ride drives round the inner wall of a hollow cylindrical chamber of siameter 20 m .If the coefficient of force friction between tyres and inner wall of a hollow cylinder is 0.5, then the minimum speed of the rider without sliding down will be
View SolutionIf a lodder weighing 250 N is placed against a smooth vertical wall having coefficient of friction between it and floor is 0.3 then what is the maximum force of friction available at the point of contact between the lodder and the floor?
View SolutionIf a lodder weighing 250 N is placed against a smooth vertical wall having coefficient of friction between it and floor is 0.3 then what is the maximum force of friction available at the point of contact between the lodder and the floor?
View Solution
