A block moving on a horizontal surface with velocity 20ms−1 comes to rest because of surface friction over a distance of 40 m. Taking g=10ms−2 , the coefficient of dynamic friction is :
0.5
0.3
0.2
0.1
The correct Answer is:A
To solve the problem of finding the coefficient of dynamic friction for a block that comes to rest due to friction, we can follow these steps:
1. Identify Given Values:
- Initial velocity, u=20m/s
- Final velocity, v=0m/s (since the block comes to rest)
- Distance, s=40m
- Acceleration due to gravity, g=10m/s2
2. Use the Third Equation of Motion:
The third equation of motion relates the initial velocity, final velocity, acceleration, and distance:
v2=u2+2as
Here, a is the retardation (negative acceleration) due to friction. Since the block comes to rest, we can rewrite the equation as:
0=(20)2+2(−a)(40)
Simplifying this gives:
0=400−80a
Rearranging gives:
80a=400⟹a=40080=5m/s2
3. Relate Retardation to Friction:
The retardation a due to friction can be expressed in terms of the coefficient of dynamic friction μk:
a=μkg
Substituting the value of g:
5=μk×10
4. Solve for the Coefficient of Dynamic Friction:
Rearranging the equation gives:
μk=510=0.5
5. Conclusion:
The coefficient of dynamic friction μk is 0.5.
Final Answer:
The coefficient of dynamic friction is μk=0.5.
---
- Initial velocity, u=20m/s
- Final velocity, v=0m/s (since the block comes to rest)
- Distance, s=40m
- Acceleration due to gravity, g=10m/s2
The third equation of motion relates the initial velocity, final velocity, acceleration, and distance:
v2=u2+2as
Here, a is the retardation (negative acceleration) due to friction. Since the block comes to rest, we can rewrite the equation as:
0=(20)2+2(−a)(40)
Simplifying this gives:
0=400−80a
Rearranging gives:
80a=400⟹a=40080=5m/s2
The retardation a due to friction can be expressed in terms of the coefficient of dynamic friction μk:
a=μkg
Substituting the value of g:
5=μk×10
Rearranging the equation gives:
μk=510=0.5
The coefficient of dynamic friction μk is 0.5.
The coefficient of dynamic friction is μk=0.5.
Similar Questions
A block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and g=10ms−2. The frictional force on the block is
View SolutionA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and g=10ms−2. The frictional force on the block is
View SolutionStarting from rest a wooden block moves with a velocity of 25ms−1 along a rough ground and comes to rest. Calculate the distance travelled by the wooden block on the rough surface of coefficient of friction 0.25.
View SolutionA 3 kg block is placed over a 10 kg block and both are palced on a smooth horizontal surface. The coefficient of friction between the block is 0.2 . If a horizontal force of 20 N is applied to 3 kg block, accelerations of the two block in ms−2 are (take, g=ms−2)

View SolutionA block slides with a velocity of 10 m/sec. on a rough horizontal surface. It comes to rest after covering of 50 m. If g is 10 m/ sec^(2) , then the coefficient of dynamic friction between the block and surface is
View SolutionA block moving on a horizontal surface with velocity 20 ms^(-1) comes to rest because of surface friction over a distance of 40 m. Taking g = 10 ms^(-2) , the coefficient of dynamic friction is :
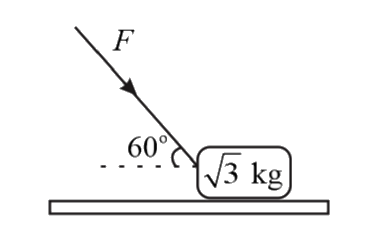
View SolutionA force F is applied on a block of mass √3kg which rests on a horizontal surface with a coefficient of friction 12√3. The maximum value of F for which the block doesn't move, is [Take g=10ms−2]
View SolutionA block of mass m is gently placed over a massive plank moving horizontal over a smooth surface with velocity 10 ms^(-1) . The coefficient of friction between the block and the plank is 0.2. The distance travelled by the block till it slides on the plank is [g = 10 ms^(-2)]
View Solution

