Match the entries of Column I and Column II.
COLUMN - I
(A) For a particle moving in a circle
(B) For a particle moving in a straight line
(C) For a particle undergoing projectile motion with the angle of projection α:0<α<π2
(D) For a particle moving in space
COLUMN - II
(P) The acceleration may be perpendicular to its velocity.
(Q) The acceleration may be in the direction of velocity
(R) The acceleration may be at some angle θ(0<θ<π2) with the velocity.
(S) The acceleration may be opposite to its velocity.
The correct Answer is:A-p, r; B-q, s; C-p, r; D=p,q r,s
To solve the problem of matching the entries from Column I with those from Column II, we will analyze each entry in Column I and determine which statement from Column II corresponds to it.
Step 1: Analyze Entry A (For a particle moving in a circle)
- In circular motion, the particle experiences centripetal acceleration directed towards the center of the circle, which is always perpendicular to the velocity of the particle (which is tangential to the circle).
- Thus, the correct match for A is P: "The acceleration may be perpendicular to its velocity."
Step 2: Analyze Entry B (For a particle moving in a straight line)
- For a particle moving in a straight line, the acceleration can be in the same direction as the velocity (causing the speed to increase) or opposite to it (causing the speed to decrease).
- Therefore, the correct matches for B are Q: "The acceleration may be in the direction of velocity" and S: "The acceleration may be opposite to its velocity."
Step 3: Analyze Entry C (For a particle undergoing projectile motion with angle of projection α:0<α<π2)
- In projectile motion, the acceleration due to gravity acts downward while the velocity has both horizontal and vertical components. At the highest point, the vertical component of velocity is zero, making the acceleration perpendicular to the horizontal velocity.
- Therefore, the correct matches for C are P: "The acceleration may be perpendicular to its velocity" and R: "The acceleration may be at some angle θ(0<θ<π2) with the velocity."
Step 4: Analyze Entry D (For a particle moving in space)
- A particle moving freely in space can have its acceleration in any direction relative to its velocity. It can be perpendicular, in the same direction, at an angle, or opposite to its velocity.
- Therefore, all statements in Column II (P, Q, R, S) are valid for D.
Final Matches:
- A → P
- B → Q, S
- C → P, R
- D → P, Q, R, S
Summary of Matches:
- A matches with P
- B matches with Q and S
- C matches with P and R
- D matches with P, Q, R, and S
- In circular motion, the particle experiences centripetal acceleration directed towards the center of the circle, which is always perpendicular to the velocity of the particle (which is tangential to the circle).
- Thus, the correct match for A is P: "The acceleration may be perpendicular to its velocity."
- For a particle moving in a straight line, the acceleration can be in the same direction as the velocity (causing the speed to increase) or opposite to it (causing the speed to decrease).
- Therefore, the correct matches for B are Q: "The acceleration may be in the direction of velocity" and S: "The acceleration may be opposite to its velocity."
- In projectile motion, the acceleration due to gravity acts downward while the velocity has both horizontal and vertical components. At the highest point, the vertical component of velocity is zero, making the acceleration perpendicular to the horizontal velocity.
- Therefore, the correct matches for C are P: "The acceleration may be perpendicular to its velocity" and R: "The acceleration may be at some angle θ(0<θ<π2) with the velocity."
- A particle moving freely in space can have its acceleration in any direction relative to its velocity. It can be perpendicular, in the same direction, at an angle, or opposite to its velocity.
- Therefore, all statements in Column II (P, Q, R, S) are valid for D.
- A → P
- B → Q, S
- C → P, R
- D → P, Q, R, S
- A matches with P
- B matches with Q and S
- C matches with P and R
- D matches with P, Q, R, and S
Similar Questions
Knowledge Check
Acceleration-time graph for a particle in translatory motion is given here.
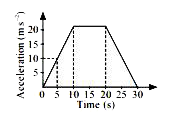
Match the quantities of column I with column II and select the correct option from given codes.
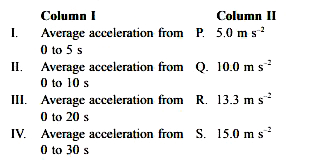 AI-S, II-P, III-R, IV-QBI-P, II-Q, III-S, IV-RCI-Q, II-P, III-R, IV-SDI-S, II-R, III-P, IV-Q
AI-S, II-P, III-R, IV-QBI-P, II-Q, III-S, IV-RCI-Q, II-P, III-R, IV-SDI-S, II-R, III-P, IV-Q
Match the corresponding entries of Column I with Column II.

View SolutionA particle is moving along a circle of a fixed radius and gaining speed in a uniform manner. Mathc columns I and II.

View SolutionMatch the entries in column I with entries in Column II and then pick out correct options.
Column I Column II

View SolutionA car is moving along a straight line. It's displacemetn (x)- time (t) grapg is shown in column II. Match the entries in column I with points on graph.

View SolutionEntries of Column-I are to be matched with entrices of Column-II. Each entry of Column-I may have the matching with one or more than entries of Column-II

View SolutionEntries of Column-I are to be matched with entrices of Column-II. Each entry of Column-I may have the matching with one or more than entries of Column-II
View SolutionEntries of Column-I are to be matched with entrices of Column-II. Each entry of Column-I may have the matching with one or more than entries of Column-II

View Solution

