A projectile is aimed at a mark on a horizontal plane through the point of projection and falls 6 m short when its elevation is 30° but overshoots the mark by 9 m when its elevation is 45∘. The angle of elevation of projectile to hit the target on the horizontal plane is :
sin−1[3√3+45]
cos−1[3√3+45]
12cos−1[3√3+410]
12sin−1[3√3+410]
The correct Answer is:D
To solve the problem, we need to find the angle of elevation (θ) for a projectile that will hit a target on a horizontal plane. We know the projectile falls short by 6 m when fired at 30° and overshoots by 9 m when fired at 45°.
1. Understanding the Range Formula:
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
where u is the initial velocity, g is the acceleration due to gravity, and θ is the angle of projection.
2. Setting Up the Equations:
- For θ=30°:
The projectile falls 6 m short, so the range can be expressed as:
R30=u2sin(60°)g=R−6
where R is the actual distance to the target.
Thus, we have:
u2⋅√32g=R−6(Equation 1)
- For θ=45°:
The projectile overshoots by 9 m, so:
R45=u2sin(90°)g=R+9
Thus, we have:
u2g=R+9(Equation 2)
3. Eliminating R:
From Equation 1:
R=u2⋅√32g+6
Substitute this expression for R into Equation 2:
u2g=⎛⎜⎝u2⋅√32g+6⎞⎟⎠+9
Simplifying gives:
u2g=u2⋅√32g+15
4. Rearranging the Equation:
Multiply through by g to eliminate the denominator:
u2=u2⋅√32+15g
Rearranging gives:
u2−u2⋅√32=15g
Factoring out u2:
u2(1−√32)=15g
Thus,
u2=15g1−√32
5. Finding sin(2θ):
Substitute u2 back into either Equation 1 or Equation 2 to find sin(2θ):
Using Equation 1:
R−6=u2⋅√32g
Substitute u2:
R−6=15g1−√32⋅√32g
Simplifying gives:
R−6=15√3/21−√32
6. Finding the angle θ:
Rearranging gives us:
sin(2θ)=R+9u2/g
Substitute u2 to find θ:
2θ=sin−1(4+3√310)
Finally, solve for θ:
θ=12sin−1(4+3√310)
Final Answer:
The angle of elevation θ to hit the target is:
θ=12sin−1(4+3√310)
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
where u is the initial velocity, g is the acceleration due to gravity, and θ is the angle of projection.
- For θ=30°:
The projectile falls 6 m short, so the range can be expressed as:
R30=u2sin(60°)g=R−6
where R is the actual distance to the target.
Thus, we have:
u2⋅√32g=R−6(Equation 1)
The projectile overshoots by 9 m, so:
R45=u2sin(90°)g=R+9
Thus, we have:
u2g=R+9(Equation 2)
From Equation 1:
R=u2⋅√32g+6
Substitute this expression for R into Equation 2:
u2g=⎛⎜⎝u2⋅√32g+6⎞⎟⎠+9
Simplifying gives:
u2g=u2⋅√32g+15
Multiply through by g to eliminate the denominator:
u2=u2⋅√32+15g
Rearranging gives:
u2−u2⋅√32=15g
Factoring out u2:
u2(1−√32)=15g
Thus,
u2=15g1−√32
Substitute u2 back into either Equation 1 or Equation 2 to find sin(2θ):
Using Equation 1:
R−6=u2⋅√32g
Substitute u2:
R−6=15g1−√32⋅√32g
Simplifying gives:
R−6=15√3/21−√32
Rearranging gives us:
sin(2θ)=R+9u2/g
Substitute u2 to find θ:
2θ=sin−1(4+3√310)
Finally, solve for θ:
θ=12sin−1(4+3√310)
The angle of elevation θ to hit the target is:
θ=12sin−1(4+3√310)
Similar Questions
A projectile is aimed at a mark on the horizontal plane through the point of projection and falls 12m short when the angle of projection is 15∘, white it overshoots the mark by 24m when the angle of projection is 45∘. Find the angle of projection to hit the mark.

View SolutionA projectile aimed at a mark, which is in the horizontal plane through the point of projection, falls a cm short of it when the elevation is α and goes b cm far when the elevation is β. Show that, if the speed of projection is same in all the cases the proper elevation is
12sin−1[bsin2α+asin2βa+b] .
View Solution
Knowledge Check
A projectile is projected and it takes 9s to reach in the horizontal plane through the point of projection. In its path it passes a point P after 4s. The height of P above the horizontal plane is
A10mB50mC100mD200mThe velocity at the maximum height of a projectile is half of its velocity of projection u. Its range on the horizontal plane is
A3u2gB√3u22gC3u2g2Du23gA projectile is required to hit a target whose co-ordinates relative to horizontal and vertical axes through the point of projection are (α,β) If the projection speed is √2gα. Then the condition when it is impossible to hit the target is
A3α>4βB3β>4αC4α>3βD4β>3α
A vertical tower stands on a horizontal plane, and from a point on the ground at a distance of 30 metres from the foot of the tower , the angle of elevation is 60∘. The height of the tower is
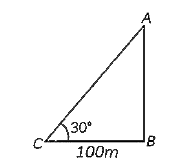
View SolutionA vertical flagstaff stands on a horizontal plane. From a point 100 m from its foot, the angle of elevation the its top is 30°. Find the height of the flqgstaf.
View SolutionA particle aimed at a target projected with an angle 15∘ with the horizontal is short of the target by 10m .If projected with an angle of 45∘ is away from the target by 15m then the angle of projection to hit the target is
View SolutionA projectile is fired at an angle of 45∘ with the horizontal. Elevation angle of the projection at its highest point as seen from the point of projection is
View SolutionA particle is projected at an angle θ with the horizontal . If angle of elevation of highest point of trajectory is ϕ when seen from point of projection, then
View Solution
