A projectile is aimed at a mark on the horizontal plane through the point of projection and falls $12 m$ short when the angle of projection is $15^{\circ}$ , white it overshoots the mark by $24 m$ when the angle of projection is $45^{\circ}$ . Find the angle of projection to hit the mark.

Video Solution

Text Solution

Verified by Experts

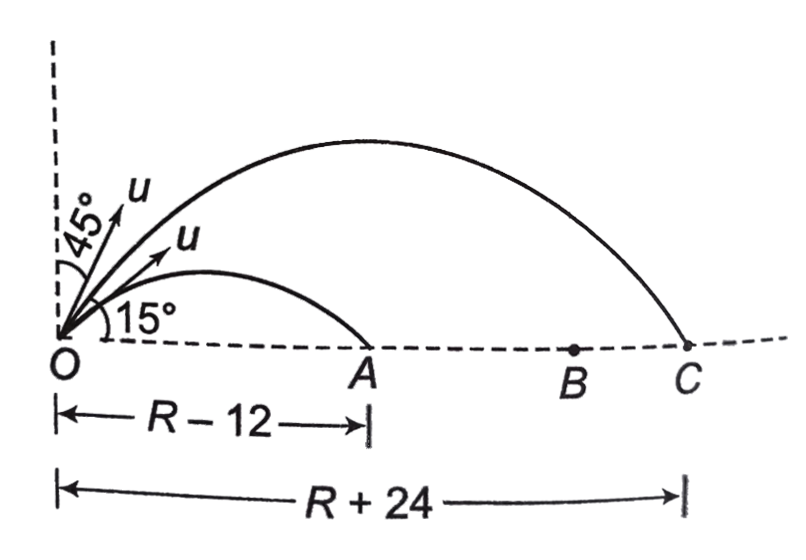
$O$ : point of projection
$B$ : location of mark
$θ_{1} = 15^{\circ}, R_{1} = R - 12$
$θ_{2} = 45^{\circ}, R_{2} = R + 24$
$R$ : Horizontal range
$R = \frac{u^{2}}{g} sin 2 θ$
$R_{1} = \frac{u^{2}}{g} sin (2 \times 15^{\circ}) = \frac{u^{2}}{2 g}$ (i)
$R_{2} = \frac{u^{2}}{g} sin (2 \times 45^{\circ}) = \frac{u^{2}}{g}$ (ii)
$\frac{R_{1}}{R_{2}} = \frac{1}{2} = \frac{R - 12}{R + 24} \Rightarrow R = 48 m$
$R = \frac{u^{2}}{g} sin 2 θ$ (iii)
Dividing (iii)by (i), we get
$\frac{R}{R_{1} = R - 12} = \frac{sin 2 θ}{\frac{1}{2}} = 2 sin 2 θ$
$\frac{48}{36} = \frac{4}{3} = 2 sin 2 θ$
$sin 2 θ = \frac{2}{3}$
$2 θ = {sin}^{- 1} (\frac{2}{3})$
$θ = \frac{1}{2} {sin}^{- 1} (\frac{2}{3})$
The angle of projection should be $\frac{1}{2} {sin}^{- 1} (\frac{2}{3})$ to hit the mark.

Updated on:21/07/2023

A projectile is aimed at a mark on a horizontal plane through the point of projection and falls 6 m short when its elevation is 30° but overshoots the mark by 9 m when its elevation is $45^{\circ}$ . The angle of elevation of projectile to hit the target on the horizontal plane is :
A ${sin}^{- 1} [\frac{3 \sqrt{3} + 4}{5}]$
B ${cos}^{- 1} [\frac{3 \sqrt{3} + 4}{5}]$
C $\frac{1}{2} {cos}^{- 1} [\frac{3 \sqrt{3} + 4}{10}]$
D $\frac{1}{2} {sin}^{- 1} [\frac{3 \sqrt{3} + 4}{10}]$
The range of a projectile for a given initial velocity is maximum when the angle of projection is $45^{\circ}$ . The range will be minimum, if the angle of projection is
A $90^{\circ}$
B $180^{\circ}$
C $60^{\circ}$
D $75^{\circ}$
A projectile is fired at an angle of $45^{\circ}$ with the horizontal. Elevation angle of the projection at its highest point as seen from the point of projection is
A $60^{\circ}$
B ${tan}^{- 1} (\frac{1}{2})$
C ${tan}^{- 1} (\frac{\sqrt{3}}{2})$
D $45^{\circ}$