A ball starts moving in a circular slot with angular acceleration at t=0 The angle between its velocity and acceleration varies with time as
The correct Answer is:B
To solve the problem step by step, we need to analyze the motion of the ball in a circular slot with the given angular acceleration.
1. Understand the Given Information:
- Angular acceleration, α=2rad/s2
- At t=0, the initial angular velocity ω0=0.
2. Determine Angular Velocity:
- The angular velocity ω at any time t can be calculated using the formula:
ω=ω0+αt
- Since ω0=0, we have:
ω=0+2t=2trad/s
3. Calculate Tangential and Centripetal Acceleration:
- Tangential Acceleration (At):
- It is given by:
At=αR=2Rm/s2
- Centripetal Acceleration (Ac):
- It is given by:
Ac=V2R=(ωR)2R=(2tR)2R=4t2R2R=4t2Rm/s2
4. Determine the Angle Between Velocity and Acceleration:
- The angle θ between the velocity vector and the resultant acceleration vector can be found using the tangent of the angle:
tanθ=AcAt
- Substituting the values of Ac and At:
tanθ=4t2R2R=4t22=2t2
5. Find θ:
- Thus, we can express θ as:
θ=tan−1(2t2)
Final Answer:
The angle between the velocity and acceleration of the ball varies with time as:
θ=tan−1(2t2)
- Angular acceleration, α=2rad/s2
- At t=0, the initial angular velocity ω0=0.
- The angular velocity ω at any time t can be calculated using the formula:
ω=ω0+αt
- Since ω0=0, we have:
ω=0+2t=2trad/s
- Tangential Acceleration (At):
- It is given by:
At=αR=2Rm/s2
- Centripetal Acceleration (Ac):
- It is given by:
Ac=V2R=(ωR)2R=(2tR)2R=4t2R2R=4t2Rm/s2
- The angle θ between the velocity vector and the resultant acceleration vector can be found using the tangent of the angle:
tanθ=AcAt
- Substituting the values of Ac and At:
tanθ=4t2R2R=4t22=2t2
- Thus, we can express θ as:
θ=tan−1(2t2)
The angle between the velocity and acceleration of the ball varies with time as:
θ=tan−1(2t2)
Similar Questions
A solid body rotates with a constant angular velocity ω0=0.50rad/s about a horizontal axis AB. At the moment t=0 the axis AB starts turning about the vertical with a constant angular acceleration β0=0.10rad/s2. Find the angular velocity and angular acceleration of the body after t=3.5s.
View SolutionA solid body rotates with angular velocity →ω=3tˆi+2t2ˆjrad/s. Find
(a) the magnitude of angular velocity and angular acceleration at time t=1s and
(b) the angle between the vectors of the angular velocity and the angular acceleration at that moment.
View Solution
Knowledge Check
A particle starts with constant angular acceleration of 2 rad/s2 in a circle of radius 4m. Find angle between net acceleration and radial acceleration after 2 s :-
Aθ=tan−1(18)Bθ=tan−1(14)Cθ=tan−1(12)Dθ=tan−1(116)A particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
A1/αB√αC1/√αDαA particle starts moving on circular path of radius 94m with tangential acceleration 3ms−2. Find angle between acceleration of the particle and radius vector at time t=1 sec.
A37∘B53∘C45∘D60∘
A particle starts moving in a non-uniform circular motion, lies angular acceleration as shown in figure. The angular velocity at the end of 4 radian is given by ω rad/s then find the value of ω.

View SolutionA particle is moving in a circular orbit when a constant tangential acceleration. After 2s from the beginning of motion, angle between the total acceleration vector and the radius E becomes 45∘. What is the angular acceleration of the particle?
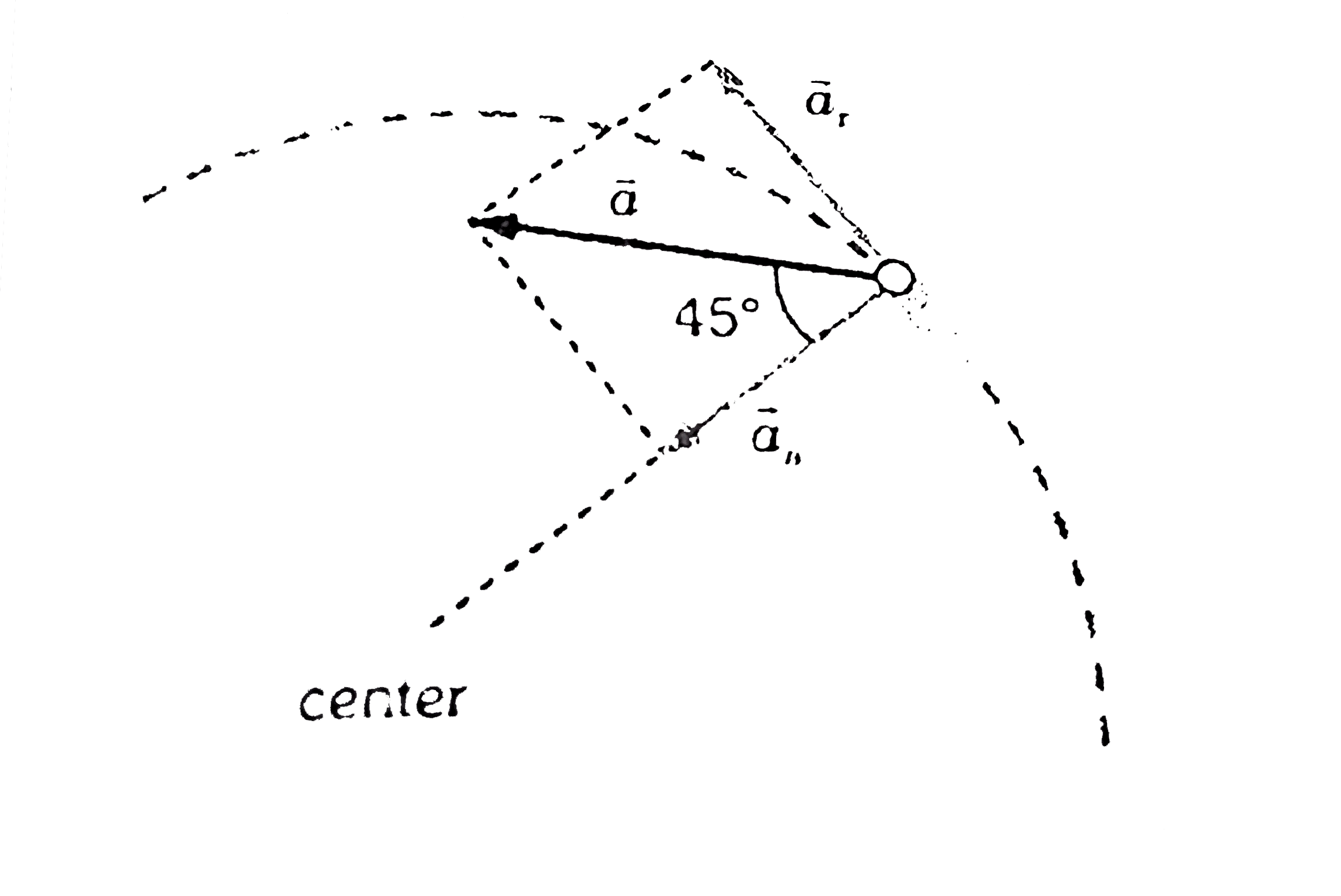
View SolutionA particle is moving in a circle of radius 0.3 . Calculate its linear acceleration at the instant when its angular velocity is 1rad/s and angular acceleration is 4rad/s2
View SolutionA solid body rotates with angular velocity ω=ati+bt2j, where a=0.50rad/s2, b=0.060rad/s3, and i and j are the unit vectors of the x and y axes. Find:
(a) the moduli of the angular velocity and the angular acceleration at the moment t=10.0s,
(b) the angle between the vectors of the angular velocity and the angular acceleration at that moment.
View SolutionOn a train moving with acceleration 10m/s2, a ball starts rolling on floor of train along the width of the train with angular acceleration 2rad/s2, radius of ball is 1m. Find the acceleration of the top point of ball at the time t=3s as seen from ground

View Solution

