Range of a projectile with time of flight 10 s and maximum height 100 m is : (g=−10m/s2)
200 m
125 m
100 m
Data incoorect
The correct Answer is:D
To solve the problem of finding the range of a projectile given the time of flight and maximum height, we can follow these steps:
Step 1: Identify the given values
- Time of flight (T) = 10 seconds
- Maximum height (H) = 100 meters
- Acceleration due to gravity (g) = -10 m/s² (we will use the positive value for calculations, g = 10 m/s²)
Step 2: Use the time of flight to find the vertical component of the initial velocity
The formula for the time of flight (T) of a projectile is given by:
T=2usinθg
Rearranging this formula to find usinθ:
usinθ=gT2
Substituting the known values:
usinθ=10×102=50 m/s
Step 3: Use the maximum height to find the vertical component of the initial velocity
The formula for maximum height (H) of a projectile is given by:
H=(usinθ)22g
Substituting the known values:
100=(usinθ)22×10
This simplifies to:
100=(50)220
Calculating the right side:
100=250020=125
This indicates a contradiction since the calculated maximum height (125 m) does not match the given maximum height (100 m).
Step 4: Conclusion
Since the calculated maximum height exceeds the given maximum height, there seems to be an inconsistency in the problem statement. Therefore, we cannot determine the range accurately based on the provided values.
Final Answer
The range cannot be determined as the given maximum height does not match the calculated maximum height based on the time of flight.
---
- Time of flight (T) = 10 seconds
- Maximum height (H) = 100 meters
- Acceleration due to gravity (g) = -10 m/s² (we will use the positive value for calculations, g = 10 m/s²)
The formula for the time of flight (T) of a projectile is given by:
T=2usinθg
Rearranging this formula to find usinθ:
usinθ=gT2
Substituting the known values:
usinθ=10×102=50 m/s
The formula for maximum height (H) of a projectile is given by:
H=(usinθ)22g
Substituting the known values:
100=(usinθ)22×10
This simplifies to:
100=(50)220
Calculating the right side:
100=250020=125
This indicates a contradiction since the calculated maximum height (125 m) does not match the given maximum height (100 m).
Since the calculated maximum height exceeds the given maximum height, there seems to be an inconsistency in the problem statement. Therefore, we cannot determine the range accurately based on the provided values.
The range cannot be determined as the given maximum height does not match the calculated maximum height based on the time of flight.
Similar Questions
A projectile is projected from ground with an initial velocity (5ˆi+10ˆj)m/s If the range of projectile is R m, time of flight is Ts and maximum height attained above ground is Hm, find the numerical value of R×HT. [Take g=10m/s2]
View SolutionIntroduction || Time OF flight, Range, Maximum Height
View Solution
Knowledge Check
Assertion In projectile motion, if time of flight is 4s, then maximum height will be 20 m. (Take, g=10ms−2)
Reason Maximum height =gT2.AIf both Asseration and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are correct but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is falseDIf Assertion is false but Reason is trueThe time of flight of a projectile is 10 s and range is 500m. Maximum height attained by it is [g=10m/s2]
A25mB50mC82mD125mA particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)A8 mB20 mC10 mD16 m
Projectile motion|| Time OF flight|| Max height|| Range
View Solution" For a projectile the ratio of the square of the time of flight to its maximum height is "
View SolutionFor a projectile if the time of flight is T, the maximum height is H and the horizontal range is R. Find the (a) the maximum height in terms of T and (b) the maximum horizontal range in terms of R and H.
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
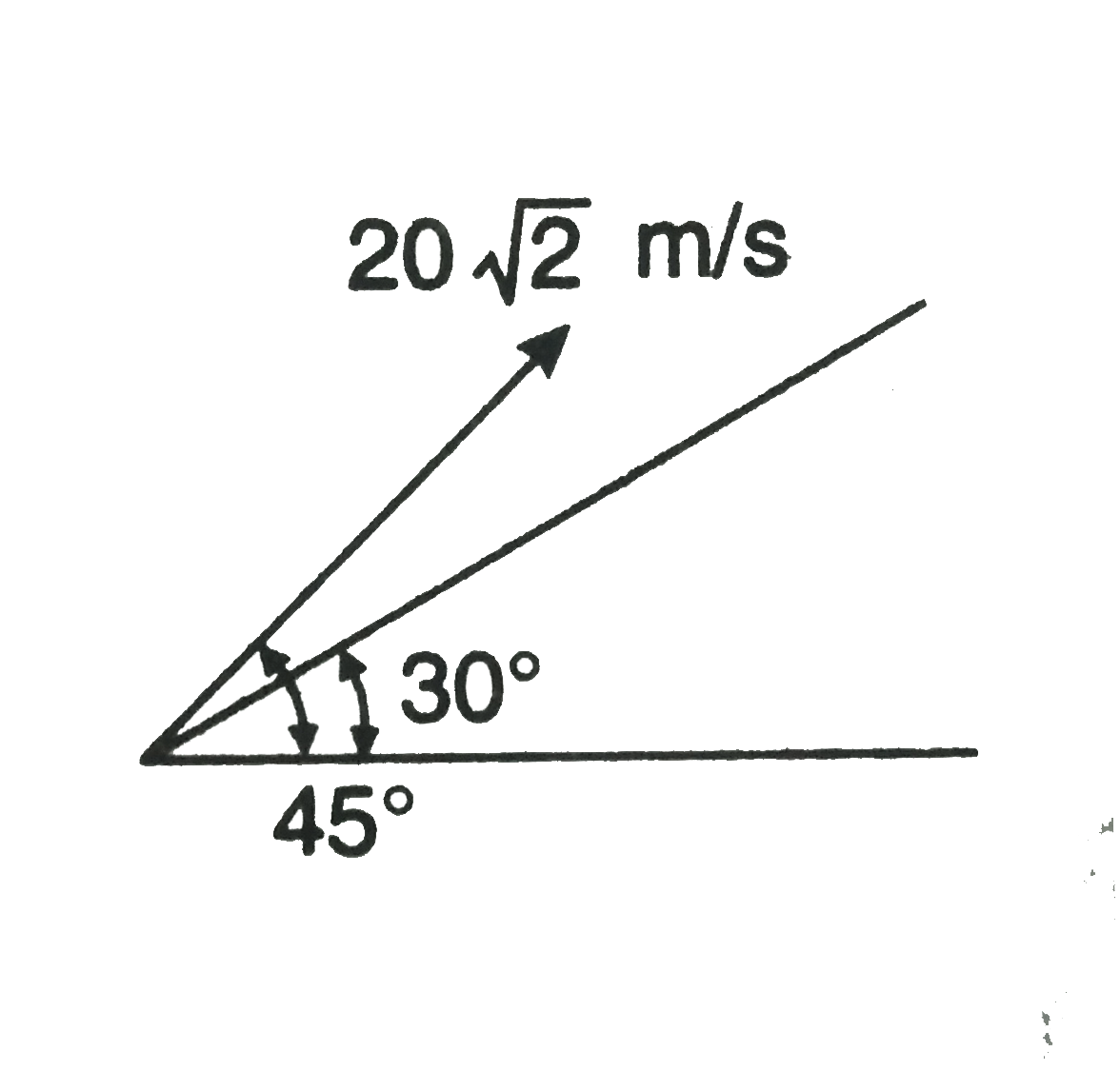
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
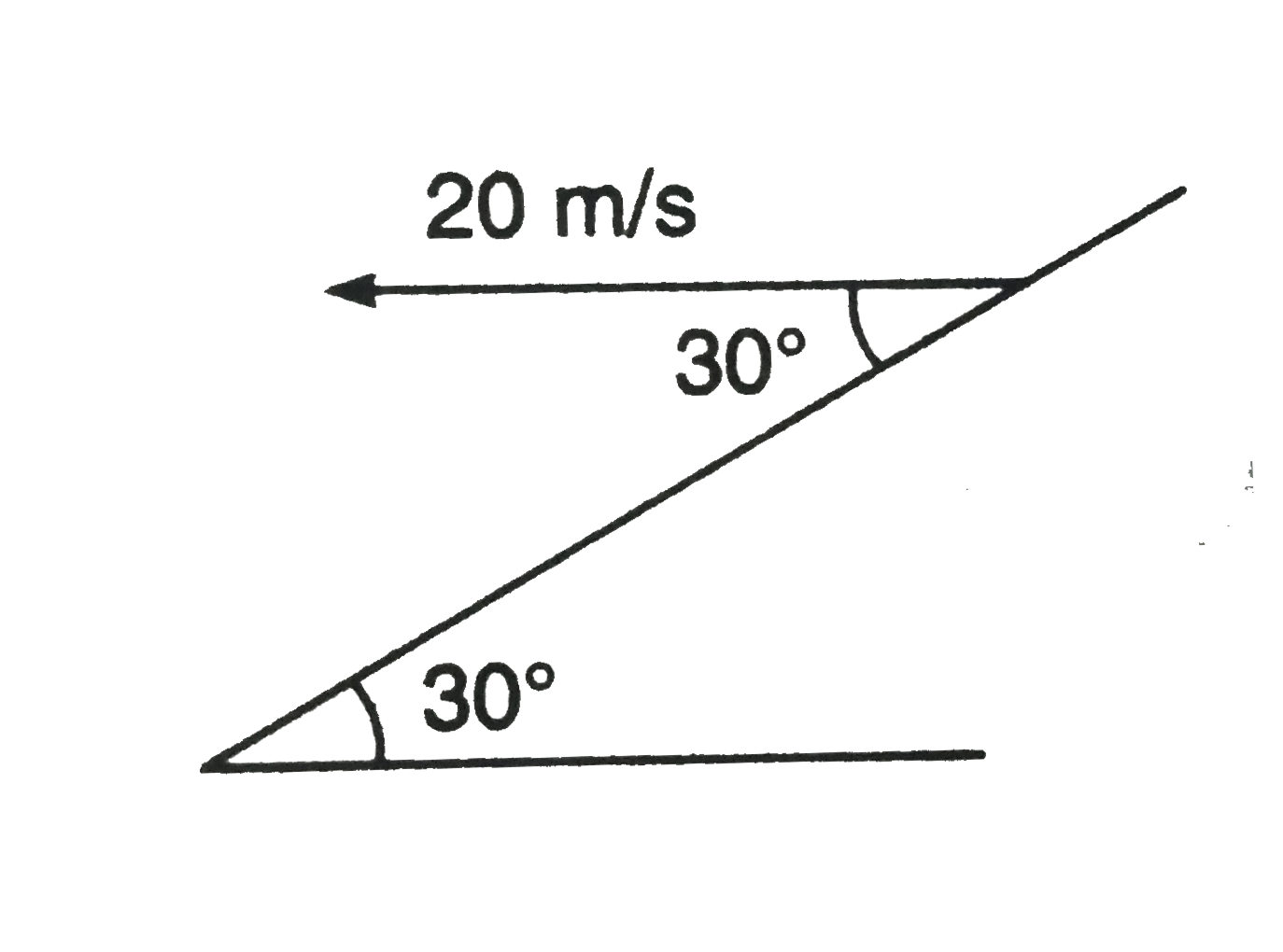
View Solution

