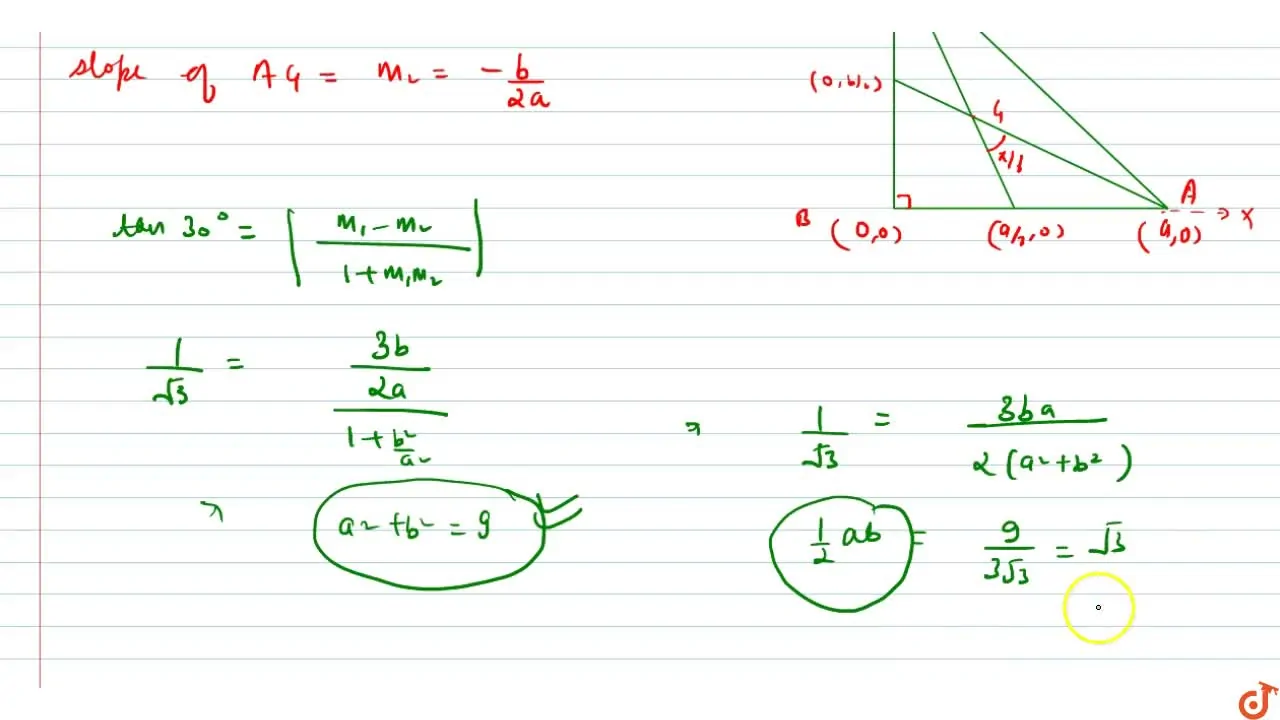
Two medians drawn from the acute angles of a right angled triangle intersect at an angle $\frac{π}{6} .$ If the length of the hypotenuse of the triangle is $3$ units, then the area of the triangle (in sq. units) is (a) $\sqrt{3}$ (b) $3$ (c) $\sqrt{2}$ (d) $9$

Video Solution

Text Solution

Verified by Experts

In the figure, ABC is right angled triangle.
Given that $A C = 3$
So, $a^{2} + b^{2} = 9$
AD and CF are two medians.
So, $D = (\frac{a}{2}, 0)$ and $F \equiv (0, \frac{b}{2})$
Slope of $A D = \frac{- 2 b}{a}$
Slope of $C F = \frac{- b}{2 a}$
$∴ tan \frac{π}{6} = ∣ ∣ ∣ ∣ ∣ \frac{\frac{- 2 b}{a} + \frac{b}{2 a}}{a + \frac{b^{2}}{a^{2}}} ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ \frac{- 3 a b}{2 (a^{2} + b^{2})} ∣ ∣ ∣ = \frac{3 a b}{9 \times 2}$
$\Rightarrow \frac{1}{\sqrt{3}} = \frac{a b}{6}$
$\Rightarrow a b = 2 \sqrt{3}$
$∴$ Area of triangle $A B C = \frac{1}{2} a b = \sqrt{3}$

Updated on:21/07/2023

Two medians drawn from acute angles of a right angled triangles intersect at an angle $π / 6$ . If the length of the hypotenuse of the triangle is 3 units, then area of the traingle (in sq. units) is
A $\sqrt{3}$
B3
C $\sqrt{2}$
D9
Two medians draen form the acute angles of a right angled triangle intersefct at an angle $\frac{π}{6} .$ If the length of the hypotenuse of the triangle is 3 units, then the area of the triangle (in sq units) is $\sqrt{K},$ then K is
A3
B $\frac{3 \sqrt{5}}{2}$
C $\sqrt{3}$
DNone of these
One acute angle of a right angle triangle is double the other. If the length of its hypotenuse is 10 cm, then its area is
A $\frac{25}{2} \sqrt{3}$
B $25 c m^{2}$
C $25 \sqrt{3} c m^{2}$
D $\frac{75}{2} c m^{2}$