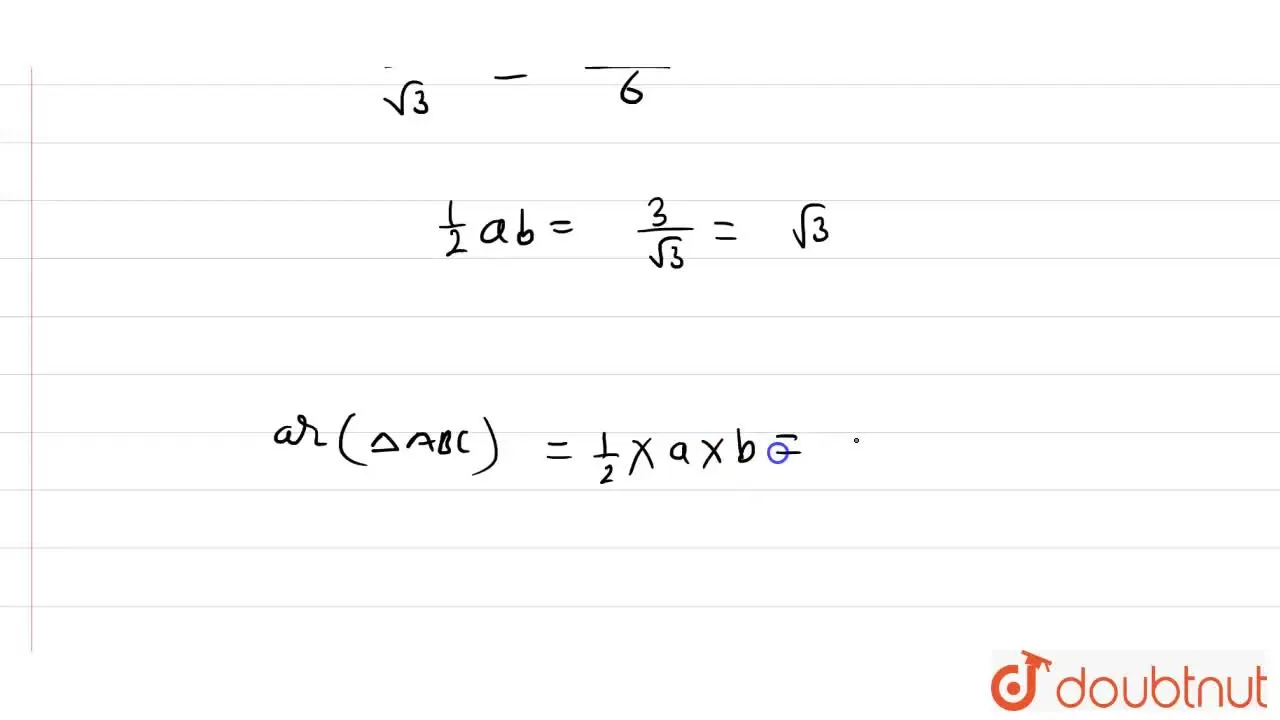Two medians drawn from acute angles of a right angled triangles intersect at an angle π/6. If the length of the hypotenuse of the triangle is 3 units, then area of the traingle (in sq. units) is
√3
3
√2
9
The correct Answer is:A
∵ AC=3⇒a2+b2=9
Slope of AD=−2ba
Slope of CF=−b2a
∴ tan.π6=∣∣
∣
∣∣−2ba+b2a1+b2a2∣∣
∣
∣∣=∣∣∣−3ab2(a2+b2)∣∣∣=3ab9×2=1√3=ab6⇒ab=2√3
ΔABC=12ab=√3
Related Playlists
Similar Questions
Two medians drawn from the acute angles of a right angled triangle intersect at an angle π6. If the length of the hypotenuse of the triangle is 3 units, then the area of the triangle (in sq. units) is (a) √3 (b) 3 (c) √2 (d) 9
View SolutionTwo medians draen form the acute angles of a right angled triangle intersefct at an angle π6. If the length of the hypotenuse of the triangle is 3 units, then the area of the triangle (in sq units) is √K, then K is
View SolutionOne acute angle of a right angle triangle is double the other. If the length of its hypotenuse is 10 cm, then its area is
View SolutionTwo acute angles of a right triangle are equal. Find the two angles.
View SolutionThe length of the two sides of a right-angled triangle are equal Find the length of the hypotenuse
View SolutionThe length of median on hypotenuse of a right angled triangle is7 cm . Find the length of the hypotenuse.
View SolutionThe hypotenuse of a right-angled isosceles triangle is 5 cm. The area of the triangle is (a) 5 cm2 (b) 6.25 cm2 (c) 6.5 cm2 (d) 12.5 cm2
View SolutionThe maximum area of a right angled triangle with hypotenuse h is
View SolutionIn a right angled triangle, one acute angle is double the other. The hypotenuse is _____ the smallest side.
View SolutionThe acute angle between the medians drawn from the acute angles of a right angle isosceles triangle is
View Solution