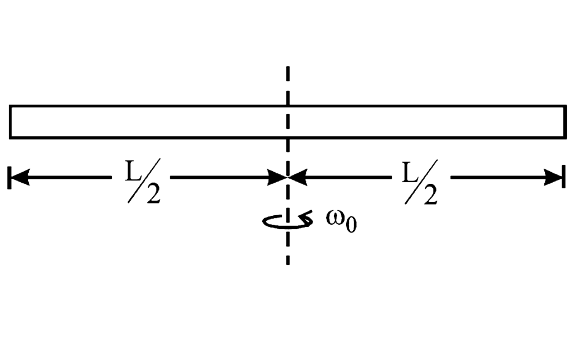
A smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity $ω_{0}$ about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

$\frac{M ω_{0}}{M + 2 m}$

$\frac{M ω_{0}}{M + 4 m}$

$\frac{M ω_{0}}{M + 6 m}$

$\frac{M ω_{0}}{M + 8 m}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Answer

Step by step video, text & image solution for A smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity omega_0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ...... by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS ROTATIONAL MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity $ω_{0}$ about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

A $ω_{0}$
B $\frac{M ω_{0}}{M + 12 m}$
C $\frac{M ω_{0}}{M + 2 m}$
D $\frac{M ω_{0}}{M + 6 m}$
Question 2 - Select One
A light rod of length l has two masses $m_{1}$ and $m_{2}$ attached to its two ends . The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is
A $\frac{m_{1} m_{2}}{m_{1} + m_{2}} l^{2}$
B $\frac{m_{1} + m_{2}}{m_{1} m_{2}} l^{2}$
C $(m_{1} + m_{2}) l^{2}$
D $\sqrt{m_{1} m_{2}} l^{2}$
Question 3 - Select One
A light rod of length $l$ has two masses $m_{1}$ and $m_{2}$ attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
A $(m_{1} + m_{2}) l^{2}$
B $\sqrt{m_{1} m_{2}} l^{2}$
C $\frac{m_{1} m_{2}}{m_{1} + m_{2}} l^{2}$
D $\frac{m_{1} + m_{2}}{m_{1} m_{2}} l^{2}$

MOTION-ROTATIONAL MOTION -Exercise - 2

Home
Ask Doubt
Profile

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

A light rod of length l has two masses m1 and m2 attached to its two ends . The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is

A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.

MOTION-ROTATIONAL MOTION -Exercise - 2

A light rod of length l has two masses $m_{1}$ and $m_{2}$ attached to its two ends . The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is

A light rod of length $l$ has two masses $m_{1}$ and $m_{2}$ attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.