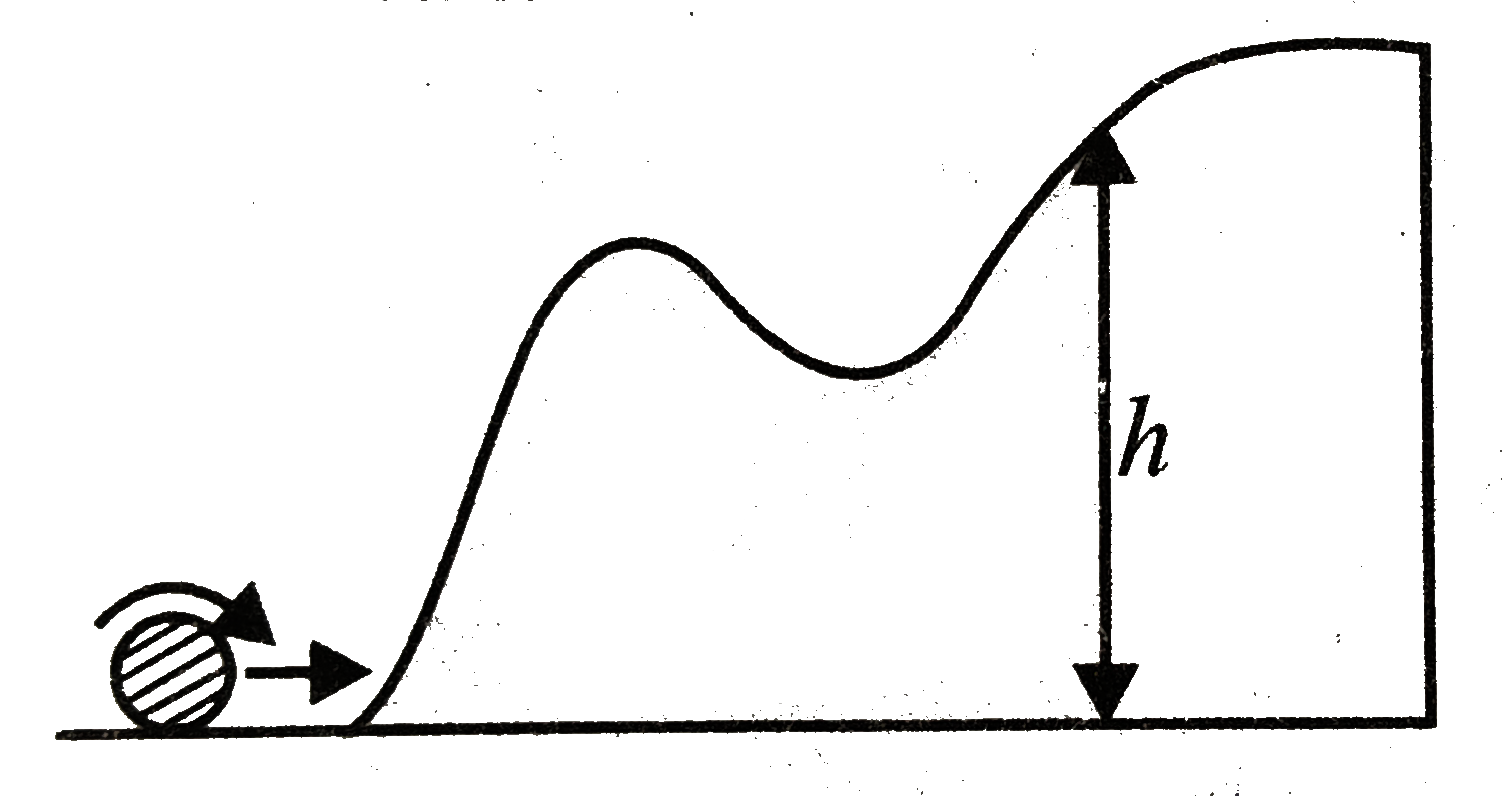
A body of mass M and radius r, rolling on a smooth horizontal floor with velocity v, rolls up an irregular inclined plane up to a vertical height (3v2/4g). Compute the moment of inertia of the body.
The total kinetic energy of the body
E=E+E=12Mv2+12Iω2
⇒E=12Mv2[1+(I/Mr2)] [asv=rω]
When it rolls up on an irregular inclined plane of height h=(3v2/4g), its KE is fully converted into PE, so by conservation of mechanical energy
12Mv2[1+1Mr2]=Mg[3v24g] which on simplification gives I=(1/2)Mr2 . This regult clearly indicates that the body is either a disc or a cylinder.
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
A solid sphere of mass 2 kg and radius R rolls on a smooth horizontal surface at 5ms−1 and then rolls up on a smooth inclined plane of inclination angle 30∘ with horizontal. Calculate the height (in m ) attained by the sphere before it stops.(Take g=10ms−2)
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View Solution
Knowledge Check
A loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
A1/2Mv2B3/2Mv2CMv2D1/2MR2ω2A body of mass M and radius R is rolling horizontally without slipping with speed v . It then rolls up a hill to a maximum height h . If h=5v26g , what is the M.I of the body ?
AMR22B23MR2C34Mr2D25MR2An object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
A25MR2BMR22CMR2D32MR2
A uniform solid sphere rolls on a horizontal surface at 20 m/s. It, then, rolls up a plane inclined at
View SolutionAn object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA ring, disc, spherical shell and solid sphere of same mass and radius are rolling on a horizontal surface without slipping with same velocity. If they move up an inclined plane, which can reach to a maximum height on the inclined plane?
View SolutionA symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
View Solution
