Two wheels A and B are placed coaxially. A has moment of inertia IA and angular velocity ωA while B is stationary. On clubbing them a clutch they move jointly by an angular velcoity 'ω' then find the M.I of 'B'
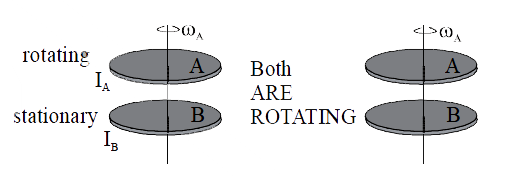
The phenomenon occurs in the absense of enternal torque, so applying law of COAM, we have
∵IAωA=(IA+B)ω⇒IB=IAωA−IAωω
=IA(ωAω−1)
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
The moment of inertia of a body moving with angular velocity ω decreases from l to l3 without any external torque. Calculate the new angular velocity of the body.
View SolutionTwo discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the entire potential energy of a spring compressed by a distance x1 Disc B is imparted an angular velocity ω by a spring having the same spring constant and compressed by a distance x2 Both the discs rotate in the clockwise direction.
The loss of kinetic energy in the above process is
View Solution
Knowledge Check
The angular momentum of a body with mass (m) moment of inertia (I) and angular velocity (ω) rad/s is equal to
AIωBIω2CIωD1ω2The relation between the torque τ and angular momentum L of a body of moment of inertia I rotating with angular velocity ω is
Aτ=dL/dtBτ=L.ωCτ=dL/dωDτ=L×ωA uniform circular disc of radius R is rotating about its own axis with moment of inertia I at an angular velocity ω if a denser particle of mass m is gently attached to the rim of disc than its angular velocity is
AωBIω(I+mR)CI+mR2IωDIωI+mR2
Two discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the entire potential energy of a spring compressed by a distance x1 Disc B is imparted an angular velocity ω by a spring having the same spring constant and compressed by a distance x2 Both the discs rotate in the clockwise direction.
The ratio x1/x2 is
View SolutionTwo discs A and B are mounted coaxially ona vertical axle. The discs have moments of inertia l and 2l respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the centre potential energy of a spring compressed by a distance x1. Disc B is imparted angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the disc rotate in the clockwise direction.
The rotation x1/(x2 is.
View SolutionTwo discs A and B are mounted coaxially ona vertical axle. The discs have moments of inertia l and 2l respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the centre potential energy of a spring compressed by a distance x1. Disc B is imparted angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the disc rotate in the clockwise direction.
The loss of kinetic energy the above process is -
View SolutionTwo discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the entire potential energy of a spring compressed by a distance x1 Disc B is imparted an angular velocity ω by a spring having the same spring constant and compressed by a distance x2 Both the discs rotate in the clockwise direction.
When disc B is brought in contact with disc A, they acquire a common angular velocity in time t. The average frictional torque on one disc by the other during this period is
View SolutionTwo discs A and B are mounted coaxially on a vertical axle. The discs have moments of inertia I and 2I respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the entire potential energy of a spring compressed by a distance x1. Disc B is imparted an angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the discs rotate in the clockwise direction.
A small object of uniform density rolls up a curved surface with an initial velocitiy v. It reaches upto a maximum height of 3v24g with respect to the initial position. The object is:
View Solution
