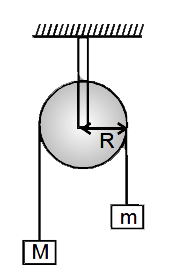
The pulley shown in figure has a moment of inertia I about it saxis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
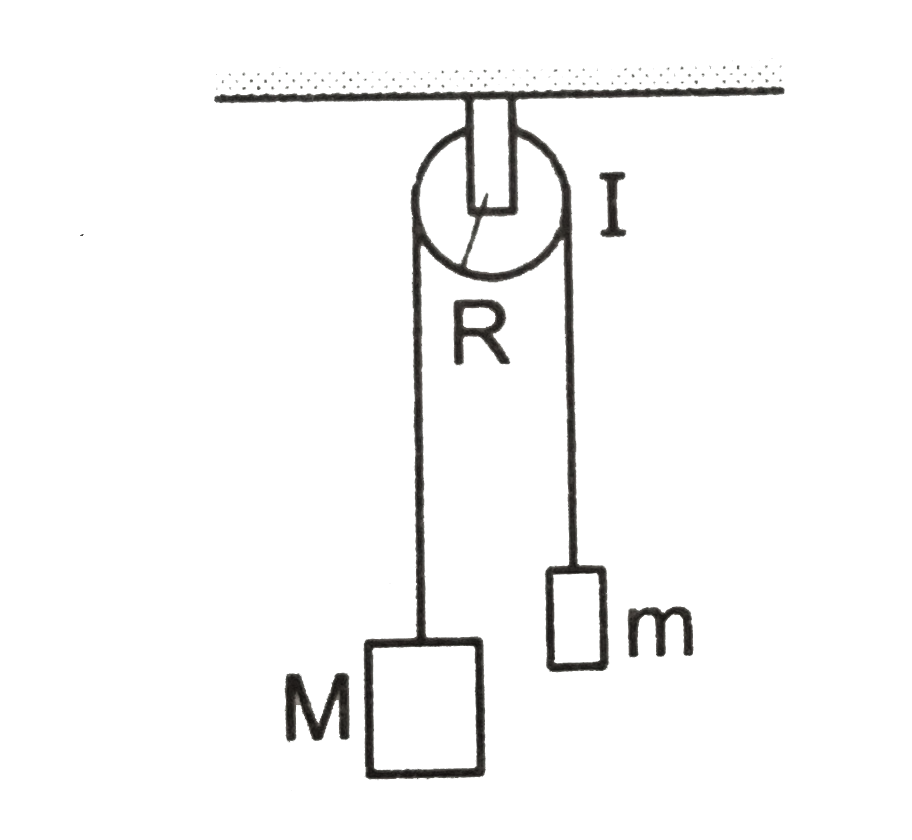
Suppose the tension in the left string is T1 and that in the right string is T2. Suppose the block of mass M goes down with an acceleration a and the other block moves up with the same acceleration. This is also the tangential acceleration of the rim of the wheel as the string does not slip over the rim.
The angular acceleration of the wheel α=aR. The equations of motion for the mass M, the mass m and the pulley are as follows ,
Mg−T1=Ma ...(1)
T2−Mg=ma ...(2)
T2R−T2R=Iα=laR ...(3)
Substituting for T1 and T2 from equations (i) and (ii) in equation (iii)
[M(g−a)−m(g+a)]R=laR
Solving, we get
a=(M−m)gR2I+(M+m)R2
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
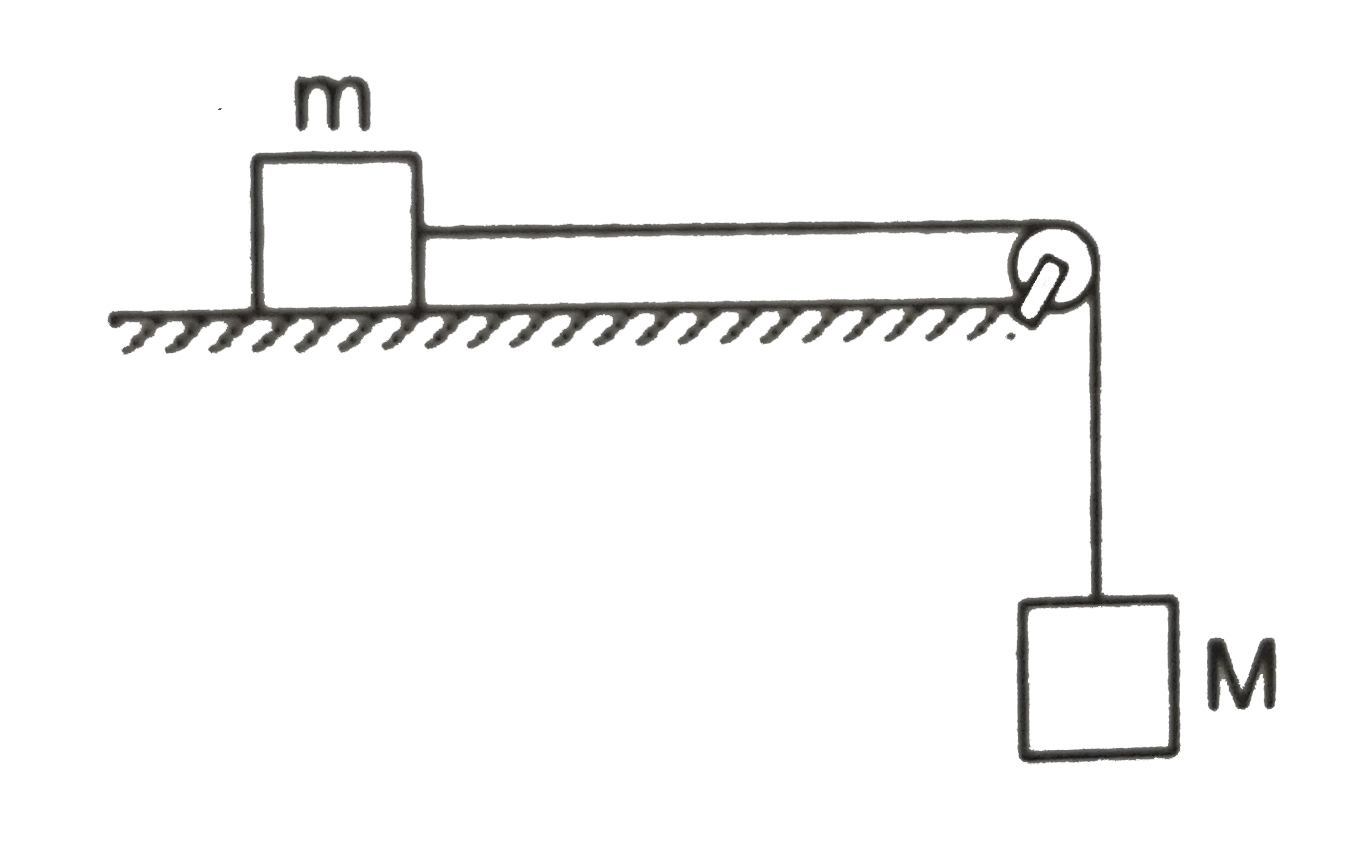
Figure shows two blocks of masses m and M connected bky a string pasing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotte about this axis. Find the accelerationof the mass M asuming that the string does not slip on the pulley.
View SolutionThe pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionThe pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionConsider the situation shown in figure. All the surfaces are frictions and the string and the pulley are light. Find the magnitude of the acceleration of the two blocks.

View SolutionAssuming the moment of inertia of the pulley to be I and its radius to be r.
View SolutionFigure shows two blocks of mass m and m connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley (uniform disc) has mass m and it can freely rotate about this axis. Find the acceleration of the mass m assuming that the string does not slip on the pulley.
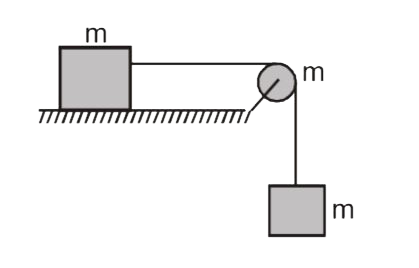
View SolutionSolve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
View SolutionThe pulleys in filgure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
View SolutionString is wrapped over a pulley and free end is fixed to the ceiling as shown in figure. Mass of the pulley is m and its radius is R. Assume that pulley is identical to dise. Calculate acceleration of pulley as it is allowed to fall by unwinding the string. Assume that string does not slip over the pulley.

View Solution
