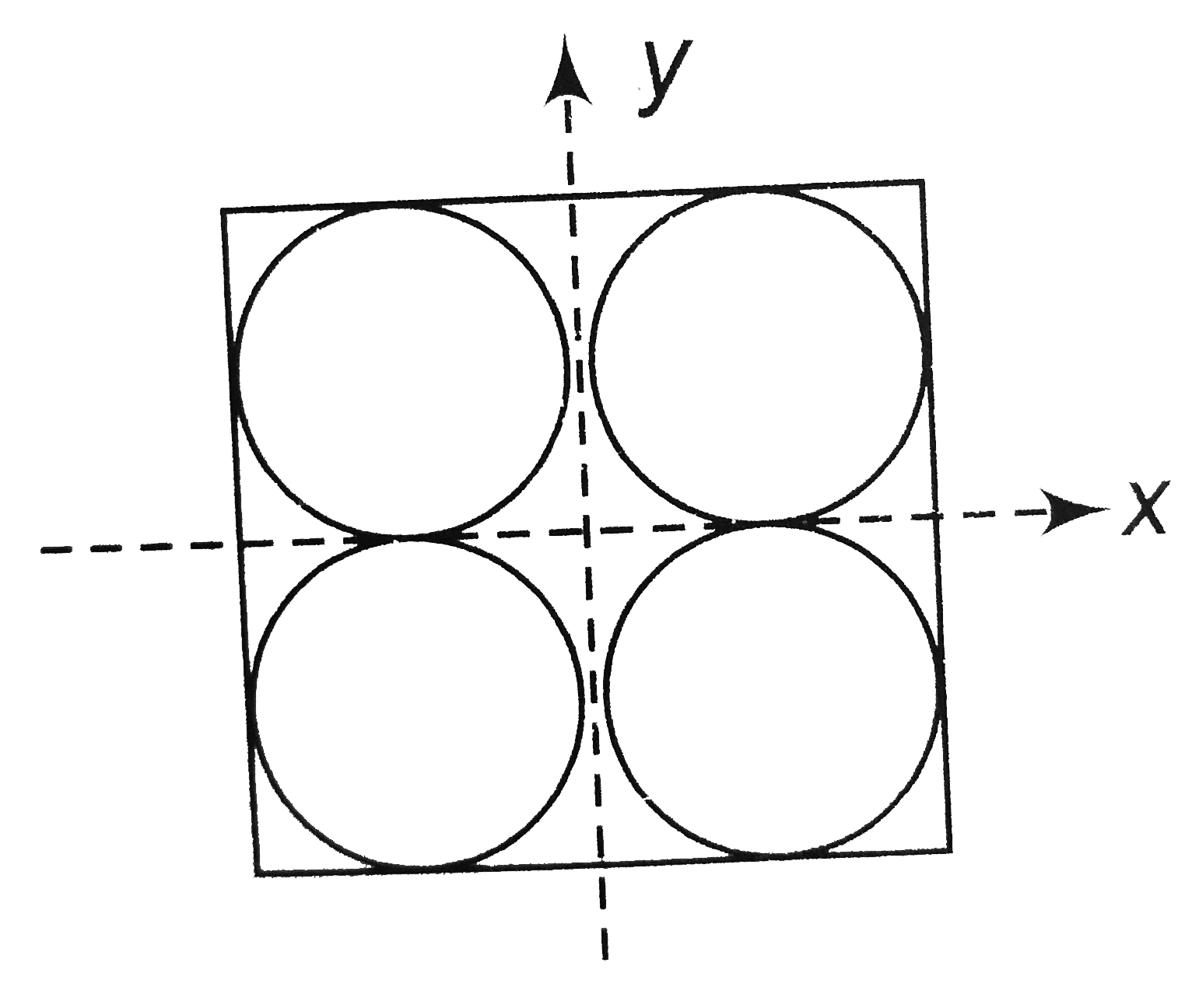
Four holes of radius R are cut from a thin square plate of side 4 R an

A concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
A $\frac{13}{24} M R^{2}$
B $\frac{11}{24} M R^{2}$
C $\frac{13}{32} M R^{2}$
D $\frac{15}{32} M R^{2}$
A concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
A $\frac{13}{24} M R^{2}$
B $\frac{11}{24} M R^{2}$
C $\frac{13}{32} M R^{2}$
D $\frac{15}{32} M R^{2}$
A hole of radius $R / 2$ is removed from a thin circular plate of radius R and mass M. The moment of inertia of the remaining plate about an axis through centre O and perpendicular to the plane of the plate is

A $\frac{3 M_{R^{2}}^{2}}{3_{2}}$
B $\frac{3 M_{R^{2}}^{2}}{13}$
C $\frac{13}{32} M R^{2}$
D $\frac{32}{13} M R^{2}$

Four holes of radius $R$ are cut from a thin square plate of side $4 R$ and mass $M$ . The moment of inertia of the remaining portion about z-axis is :
.