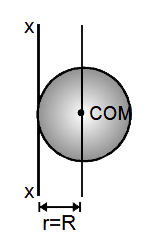
Find the moment of inertia of a solid sphere of mass M and radias R about an axis XX shown in figure. Also find radius of gyration about the given axis.
Video Solution
Text Solution
From theorem of parallel axis,
IXX=ICOM+Mr2
=25MR2+MR2
=75MR2
|
Topper's Solved these Questions
- ROTATIONAL MOTION Book:MOTIONChapter:ROTATIONAL MOTION Exercise:Exercise - 1
Explore 90 Videos
- ROTATIONAL MOTION Book:MOTIONChapter:ROTATIONAL MOTION Exercise:Exercise - 2
Explore 40 Videos
- RAY OPTICSBook:MOTIONChapter:RAY OPTICSExercise:Exercise-4
Explore 38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBook:MOTIONChapter:SEMI CONDUCTOR AND LOGIC GATESExercise:EXERCISE 3
Explore 34 Videos
Similar Questions
Knowledge Check
The moment of inertia of a solid sphere of mass ‘M' and radius 'R' about a tangent to the sphere is
A25MR2B63MR2C45MR2D75MR2Moment of inertia of a hollow cylinder of mass M and radius r about its own axis is
A23Mr2BMr2C13Mr2D12Mr2Moment of inertia of a hollow cylinder of mass M and radius R, about the axis of cylinder is
A12MR2BMR2C23MR2D25MR2
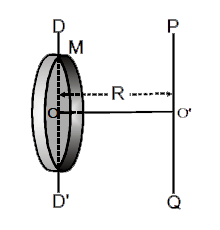
Find the moment of inertia of solid sphere of mass M about a diameter as shown in Fig.
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionFind moment of inertia of a uniform solid sphere (mass m, radius r) about a tangent.
View SolutionFind the moment of inertia of a uniform sphere of mass m and radius R about a tangent if the spheres (1) solid (ii) hollow?
View SolutionThe radius of gyration of a solid cylinder of mass M and radius R about its own axis is
View Solution