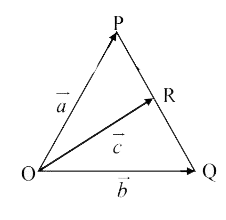
If PR = RQ, then :
→A+→b=2→C
→A−→b=→C
→A−→b=2→C
→A+→b=→C
The correct Answer is:a
¯c=¯a+¯¯¯PR but ¯¯¯PR=¯¯¯RQ (equal in magnitude same in direction)
→¯c−¯a=¯b−¯c→¯a+¯b=2¯c
Similar Questions
In △ABC, P and Q are the middle points of the sides AB and AC respectively. R is a point on the segment PQ such that PR: RQ =1: 2. If PR = 2cm, then BC =?
△ABC में, P और Q क्रमशः भुजाओं AB तथा AC के मध्य बिंदु हैं। R, PQ पर एक बिंदु इस प्रकार है कि PR: RQ =1: 2 यदि PR=2 सेमी, तो BC=
View SolutionIf S is the midpoint of a straight line PQ and R is a point different from S, such that PR = RQ then
View Solution
Knowledge Check
In ΔPQR, the equation of the internal angle bisector of angle Q is y = x and the equation of side PR is 3x−y=2. If coordinates of P are (3, 2) and 2PQ=RQ, then the coordinates of Q are
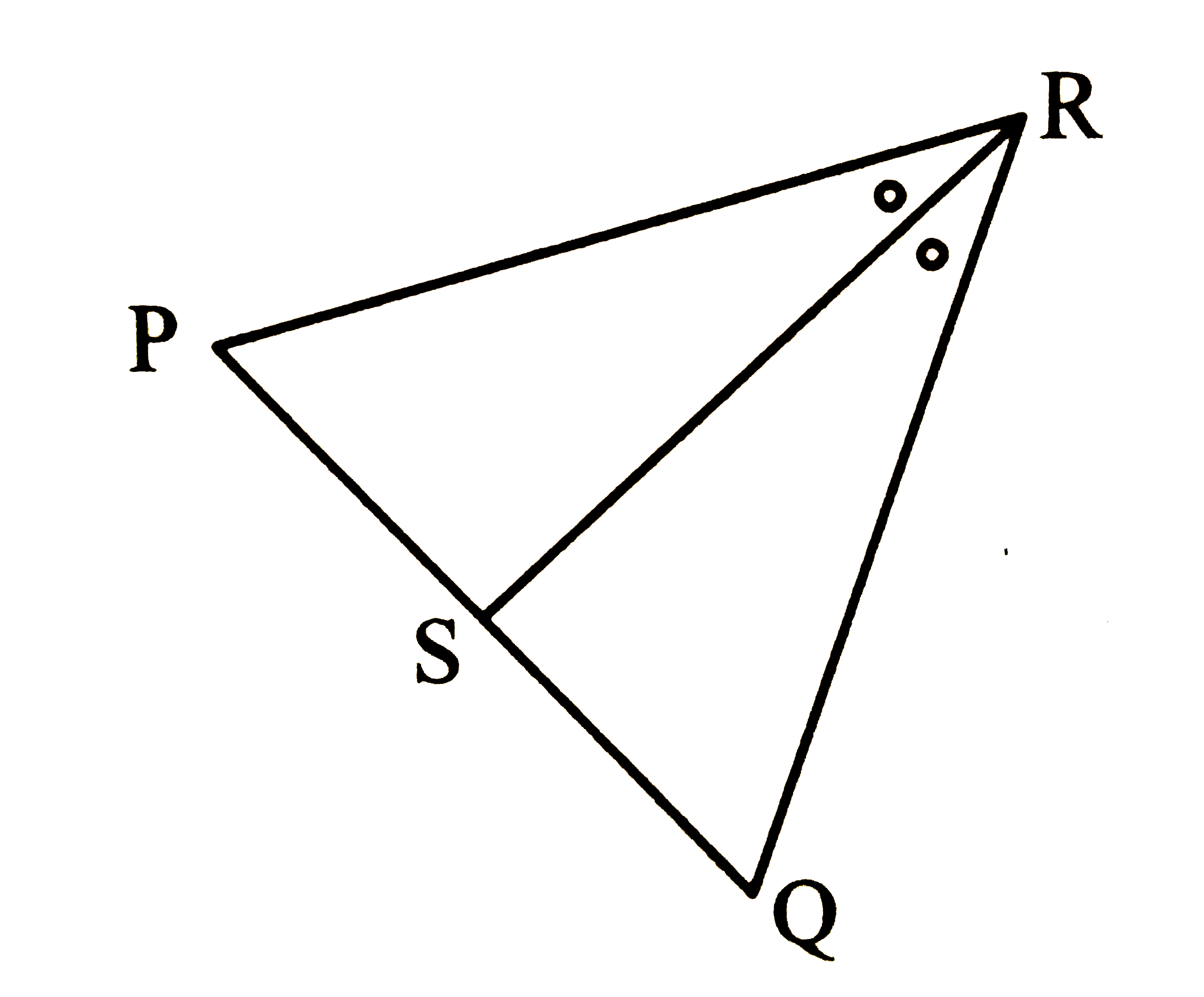
A(3, 3)B(7, 7)C(−2,−2)D(5, 5)If S is the midpoint of a straight line PQ and R is a point different from S , such that PR = RQ , then
A∠PRS=90∘B∠QRS=90∘C∠PSR=90∘D∠QSR<90∘RQ is
AC/NBN/CCCO2/O2DO2/CO2
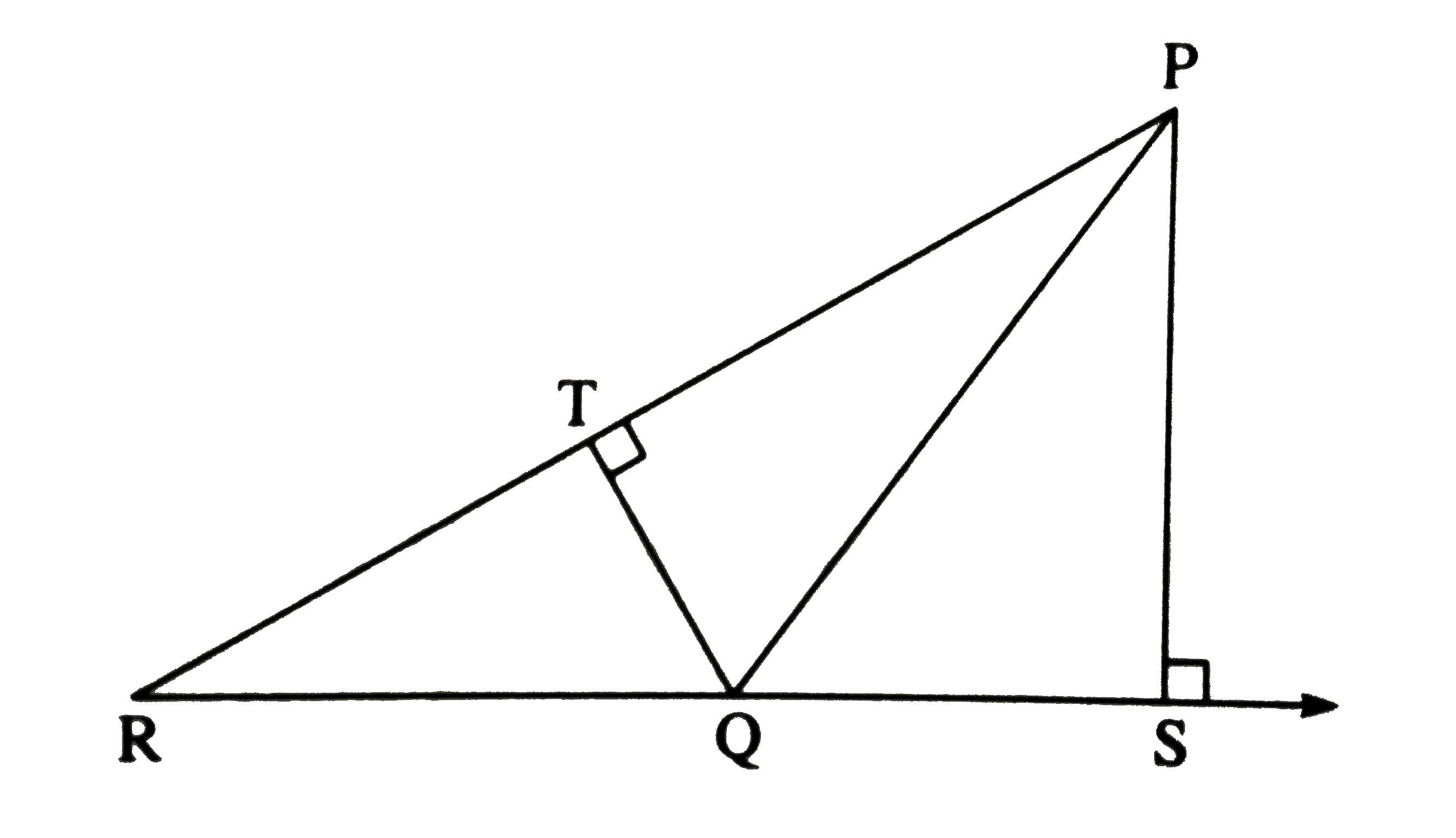
In the following figure set PS⊥ seg RQ,set QT⊥ set PR. If RQ=6,PS=6 and PR=12, then find the QT.
View SolutionIn ΔPQR, seg RS bisects ∠R.if PR = 15, RQ = 20, PS = 12 , then find SQ.
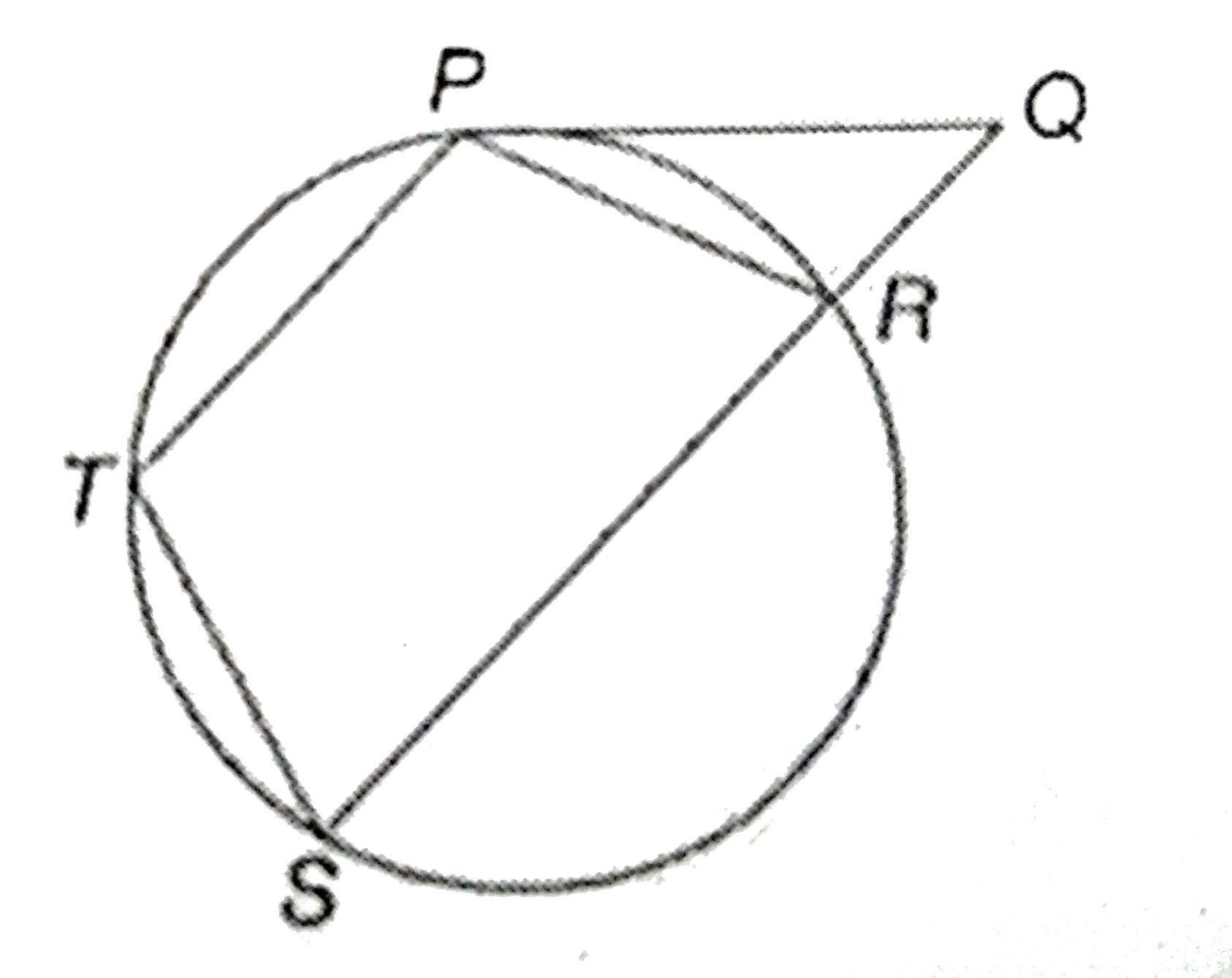
View SolutionIn the figure above (not to scale), PQ is a tangent segment to the circle at P.If P,R,S and T are concyclic points, ∠QPR=40∘ and PR=RQ then find ∠PTS.
View SolutionLet PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. PS and RQ intersect at a point X on the circumference of the circle. If PQ = 9 and RS = 4, then the diameter of the circle is :
View SolutionRQ is
View Solution
