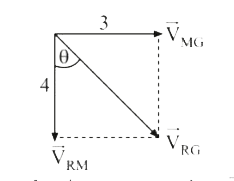
A man walking with 3 m/s feels the rain falling vertically with a speed of 4 m/s. Find the angle which the rainfall makes with the vertical according to a stationary observer.
37∘
53∘
tan−1(35)
tan−1(53)
The correct Answer is:a
→VRG=→VRM+→VMG
tanθ=34
θ=37∘
Similar Questions
A man moving with 5ms−1 observes rain falling vertically at the rate of 10ms−1. Find the speed and direction of the rain with respect to ground.
View SolutionA man moving with 5ms−1 observes rain falling vertically at the rate of 10ms−1. Find speed of the rain with respect to ground.
View SolutionA man is walking with 3m/s, due east. Rain is falling vetically downwards with speed 4m/s. Find the direction in which man should hold his umbrella, so that rain does not wet him.
View SolutionA man running with velocity 3m/s finds that raindrops are hitting him vertically with a speed of 4m/s.
Raindrops are falling at an angle θ with the vertical. Value of θ isView SolutionA man running with velocity 3m/s finds that raindrops are hitting him vertically with a speed of 4m/s.
Magnitude of velocity of the raindrops isView SolutionA man is walking on a level road at a speed of 3.0 km/h. Rain drops fall vertically wth a sped of 4.0 km/h. Find the velocity of the raindrops with respect to the man.
View SolutionA man running on the horizontal road at 8kmh−1 find the rain appears to be falling vertically. He incresases his speed to 12kmh−1 and find that the drops make angle 302 with the vertical. Fin dthe speed and direction of the rain with respedt to the road.
View SolutionTo a man going with a speed of 5ms−1, rain appears to be falling vertically. If the actual speed of rain is 10ms−1, then what is the angle made by rain with the vertical ?
View SolutionA man running on a horizontal road at 6km/h finds the rain falling vertically. He doubles his speed and find that the raindrops make an angle 37∘ with the vertical. Find the velocity of rain with respect to the ground.
View SolutionA person walking ,on a horizontal road at 2 km/h finds that the rain is falling vertically . Now the person increasses his speed to 4 km/h and find that rain makes an angle 45∘ with the vertical . Find the velocity of rain with respect to the road.
View Solution


