Consider the following statements for an electron moving in nth orbit of hydrogen like species of atomic number Z?
I. Kinetic energy ∝Z2n2
II. Frequency of revolution ∝Z2n3
III. Coulombic force of attraction ∝Z3n4
IV. Momentum ∝Zn
The correct choice is :
I, II, IV
I, III
II, III
I, II, III, IV
The correct Answer is:D
(a) K.E.∝v2, K.E.∝(Zn)2
(b) Frequency ∝1T∝v2πr∝(Zn)Zn2,f∝(Z2n3)
(c) F∝q1q2r2∝(z3n4)
(d) momentum ∝v∝(zn)
Similar Questions
The energy of an electron moving in nth Bohr's orbit of an element is given by En=−13.6n2Z2 eV/ atom (Z=atomic number). The graph of E vs. Z2 (keeping "n" constant) will be :
View SolutionBohr's model enables us to derive the energy of an electron revolving in nth orbit. For H-atom and hydrogen like species :
En=2π2me4Z2n2h2
or =−13.6Z2n2eVatom−1=21.8×10−19Z2n2Jatom−1
This helps to calculate the radius of an orbit,
rn=0.529n2ZÅ
Bohr's model also explains the occurrence of different spectral lines. The wavelengths of difference line can be given as :
1λ=¯v(incm−1)=R(1n21−1n22)
R=109678cm−1andn2>n1.
What is the ratio of radius of 4th orbit of hydrogen and 3rd orbit of Li2+ ion ?
View Solution
Knowledge Check
According to Bohr's atomic energy :-
(A) Kinetic energy of electron is ∝Z2n2.
(B) The product of velocity (v) of electron and principal quantum number(n), 'vn'∝Z2.
(C) Frequency of revolution of electron in an orbit is ∝Z3n3.
(D) Coulombic force of attraction on the electron is ∝Z3n4.
Choose the most appropriate answer from the option given below:A(C) onlyB(A) onlyC(A),(C) and (D) onlyD(A) and (D) onlyRadius (rn) of electron in nth orbit versus atomic number (Z) graph is
A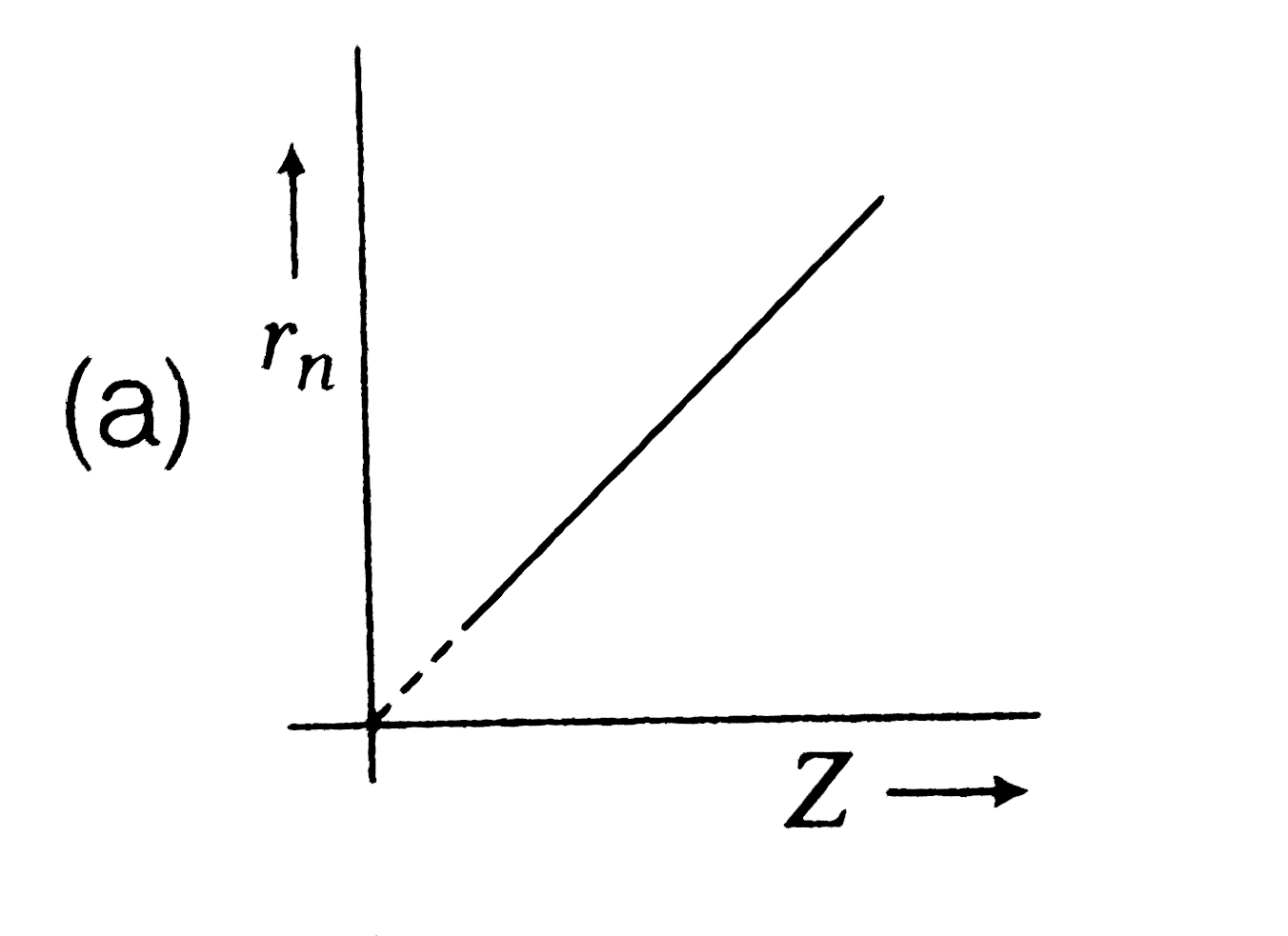 B
B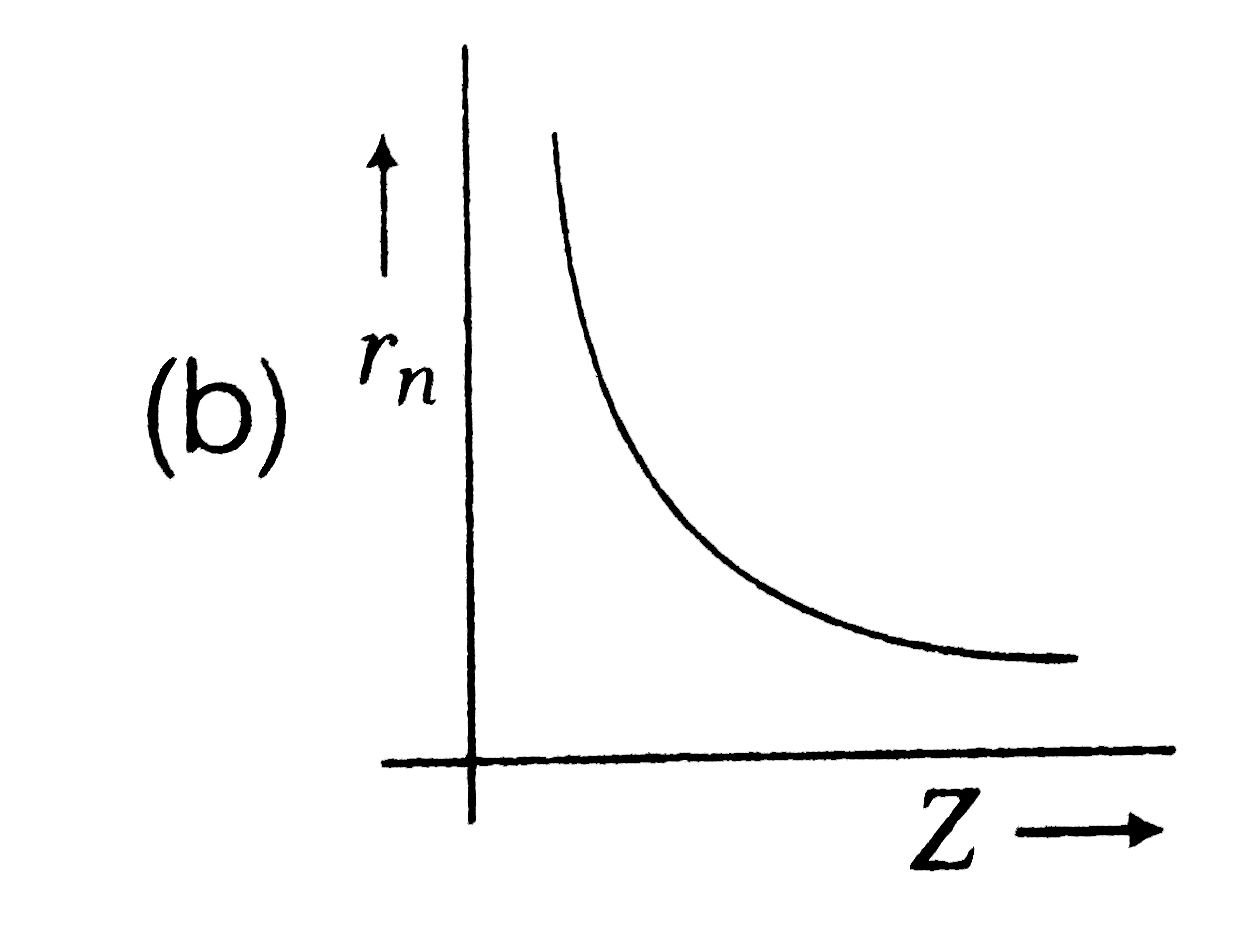 C
C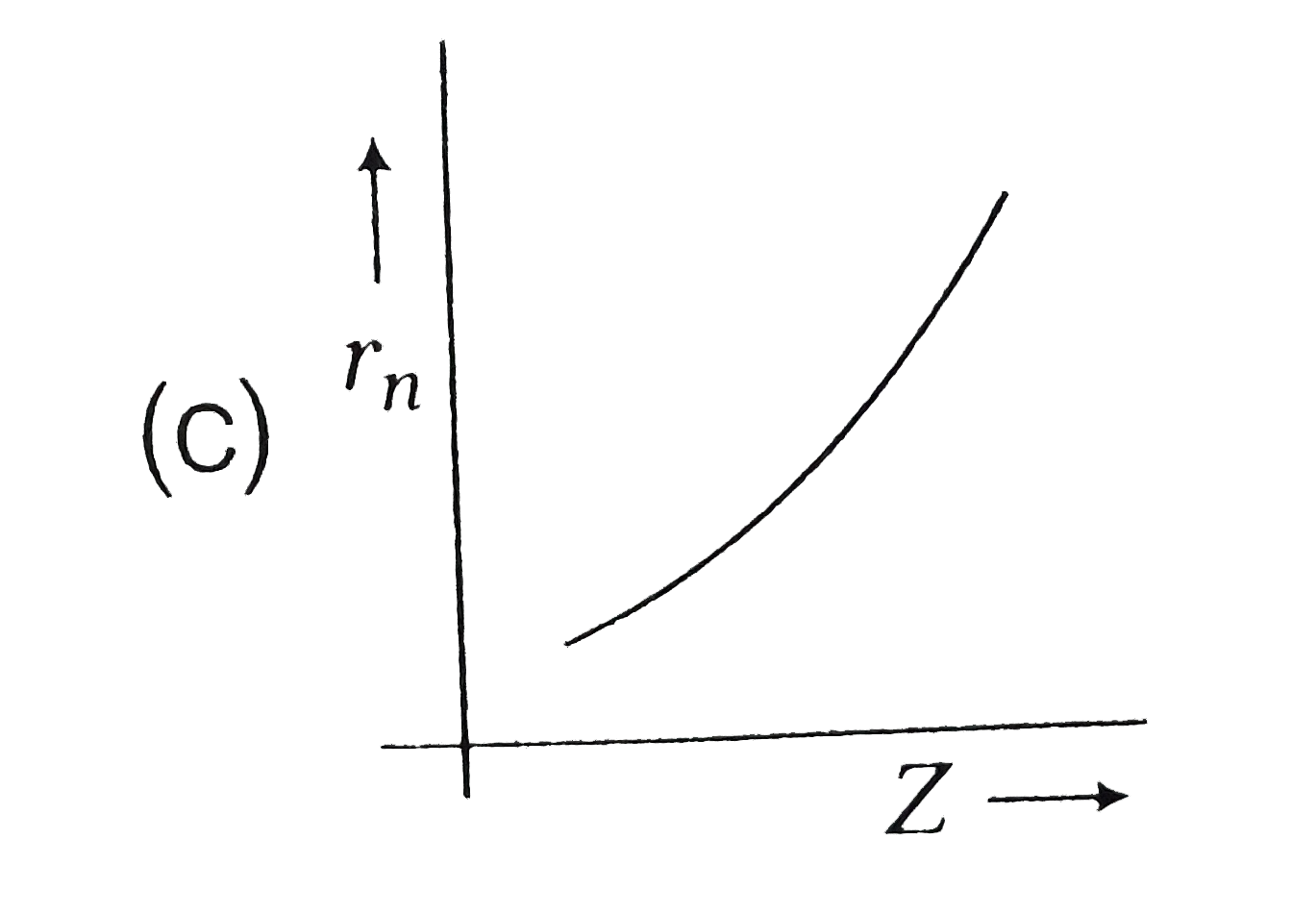 D
D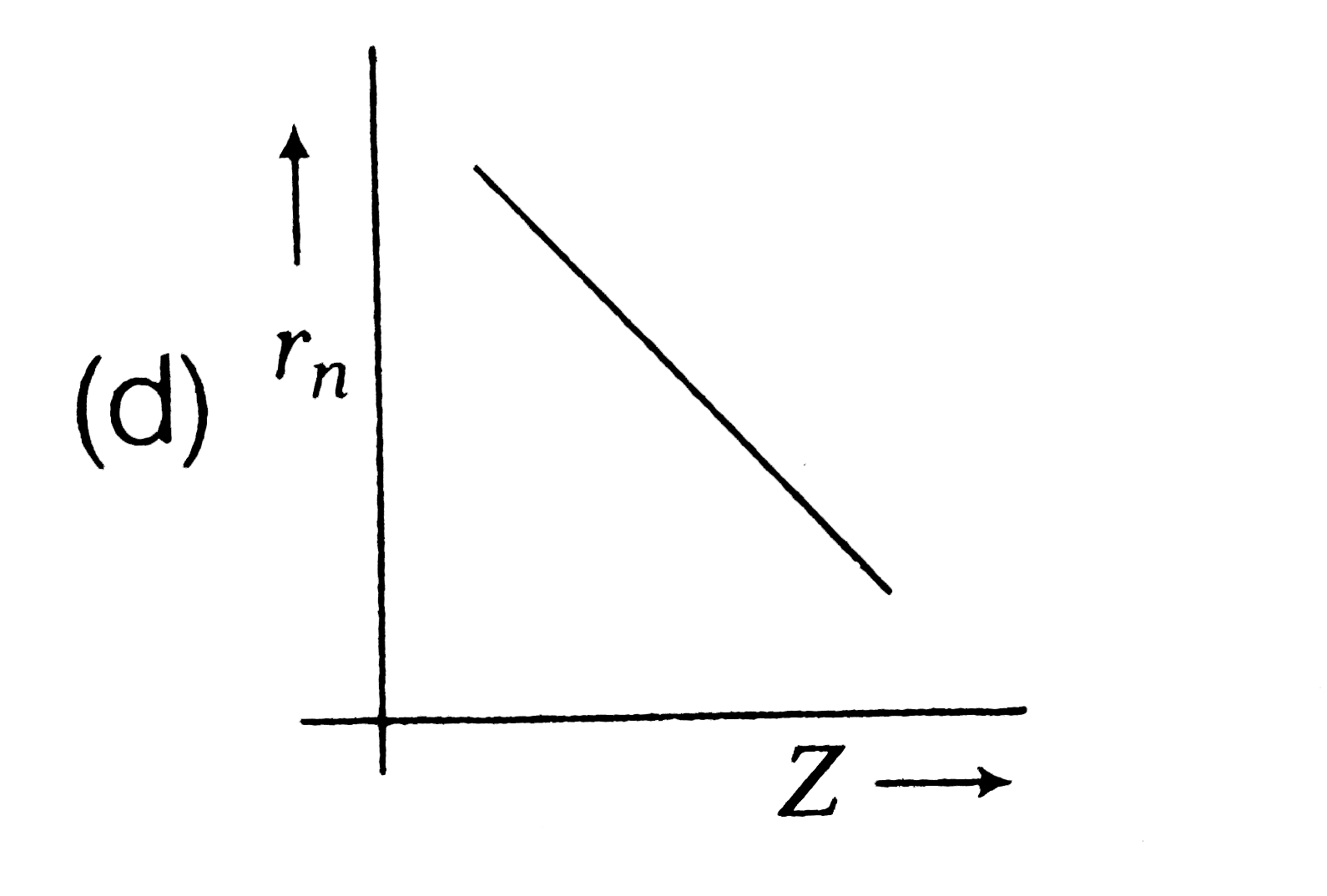
Time period of revolution of an electron in nth orbit in a hydrogen like atom is given by T=T0naZb,Z=atomic number
AT0=1.5×10−16s,a=3BT0=6.6×1015s,a=3CT0=1.51×10−16s,b=3DT0=6.6×1015s,b=3
Bohr's model enables us to derive the energy of an electron revolving in nth orbit. For H-atom and hydrogen like species :
En=2π2me4Z2n2h2
or =−13.6Z2n2eVatom−1=21.8×10−19Z2n2Jatom−1
This helps to calculate the radius of an orbit,
rn=0.529n2ZÅ
Bohr's model also explains the occurrence of different spectral lines. The wavelengths of difference line can be given as :
1λ=¯v(incm−1)=R(1n21−1n22)
R=109678cm−1andn2>n1.
What is the experimental evidence in support of the fact that electronic energies in an atom are quantized ?
View Solutionrn,z= Radius of nth orbit of a single electron species having atomic number 'z'
un,z= Velocity of electron in nth orbit of a single electron specie having atomic number 'z'
En,z= Magnitude of total energy of electron in nth orbit of a single electron species having atomic number 'z'.
Kn,z= Magnitude of kinetic energy of electron in nth orbit of a single electron species having atomic number 'z'
Pn,z= Magnitude of potential energy of electron in nth orbit of a single electron species having atomic number 'z'
fn,z= Frequency of electron in nth orbit of a single electron species having atomic number 'z'.
Tn,z= Time period of electron in nth orbit of a single electron species having atomic number 'z'
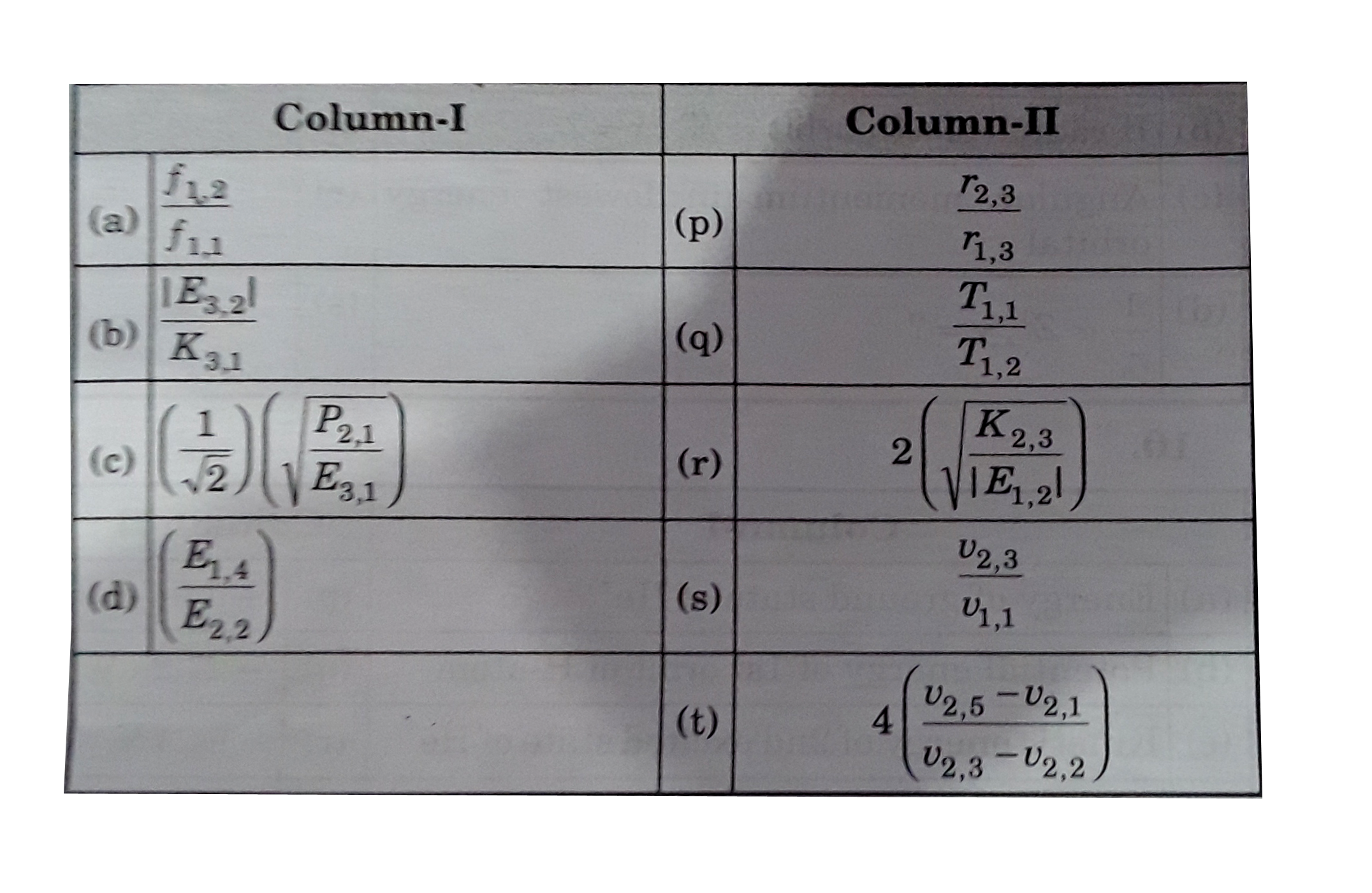
View SolutionThe energy of an electron in the nth Bohr orbit of hydrogen atom is
View SolutionConsider the following statements
I Energies of the orbitals in hydrogen or hydrogen like species depend only on the quantum number 'n'
II Energies of the orbitals in multi-electron atoms depend on quantum numbers 'n' and 't'
View SolutionWhich of the following is correct regarding Bohr's theory for hydrogen like atoms in nth orbit
Time period : Tn=2πrnvn
Kn=−En:Un=2En
rn∝n2Z,vn∝Zn,Tn∝n3Z2,En∝Z2n2
Angular momentum is independent of Z
View Solution
