Which of the following is correct regarding Bohr's theory for hydrogen like atoms in orbit
Time period :
Angular momentum is independent of Z
(i), (ii), (iii)
(i),(ii),(iv)
(i), (iii),(iv)
all
The correct Answer is:D
Step by step video, text & image solution for Which of the following is correct regarding Bohr's theory for hydrogen like atoms in n^(th) orbit Time period : T_(n)=(2pir_(n))/(v_(n)) K_(n)=-E_(n) : U_(n)=2E_(n) r_(n) prop (n^(2))/(Z) , v_(n) prop (Z)/(n) , T_(n) prop (n^(3))/(Z^(2)) , E_(n) prop (Z^(2))/(n^(2)) Angular momentum is independent of Z by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Consider the following statements for an electron moving in nth orbit of hydrogen like species of atomic number Z?
I. Kinetic energy ∝Z2n2
II. Frequency of revolution ∝Z2n3
III. Coulombic force of attraction ∝Z3n4
IV. Momentum ∝Zn
The correct choice is :AI, II, IVBI, IIICII, IIIDI, II, III, IVIn hydrogen atom, the radius of nth Bohr orbit is Vn. The graph Beetween log.(rnr1) will be
A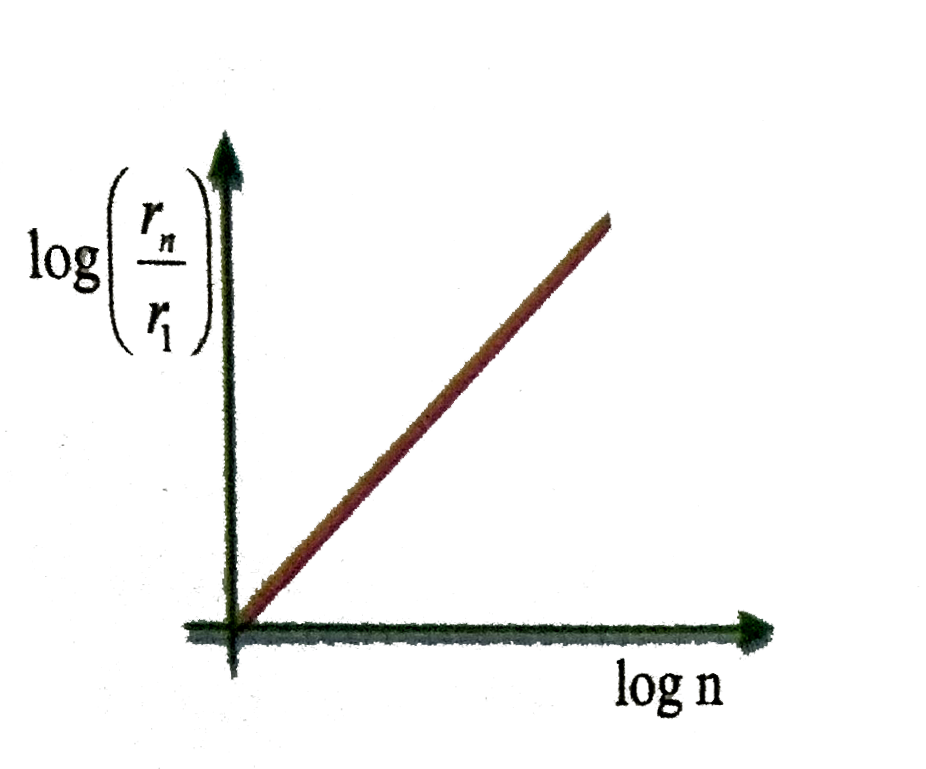 B
B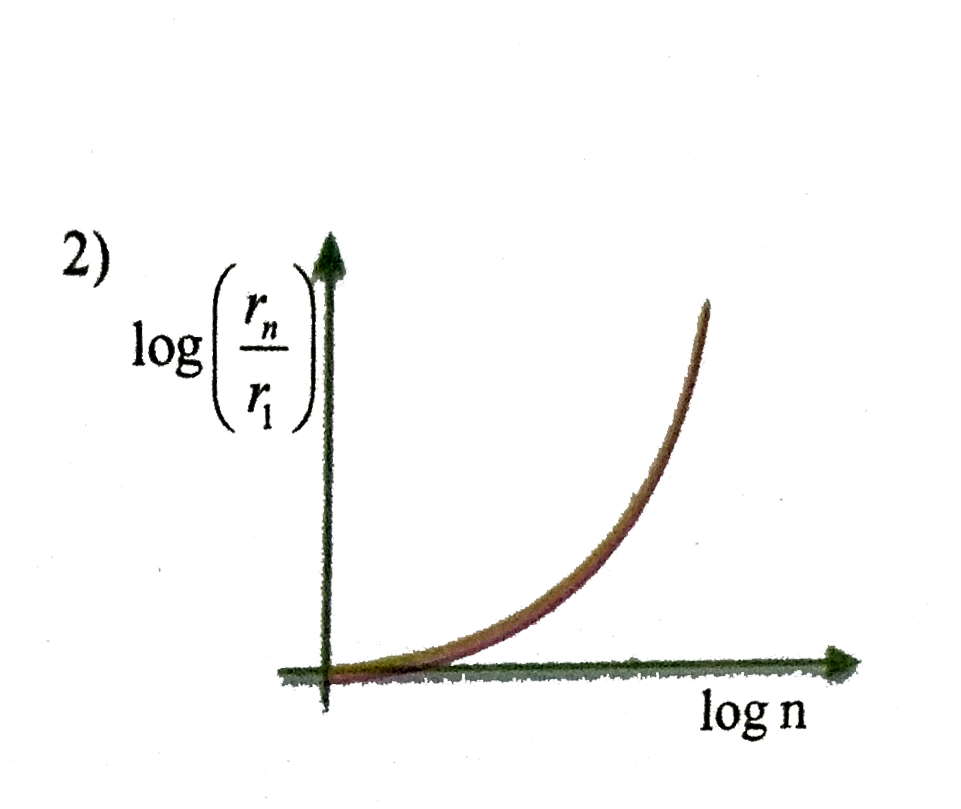 C
C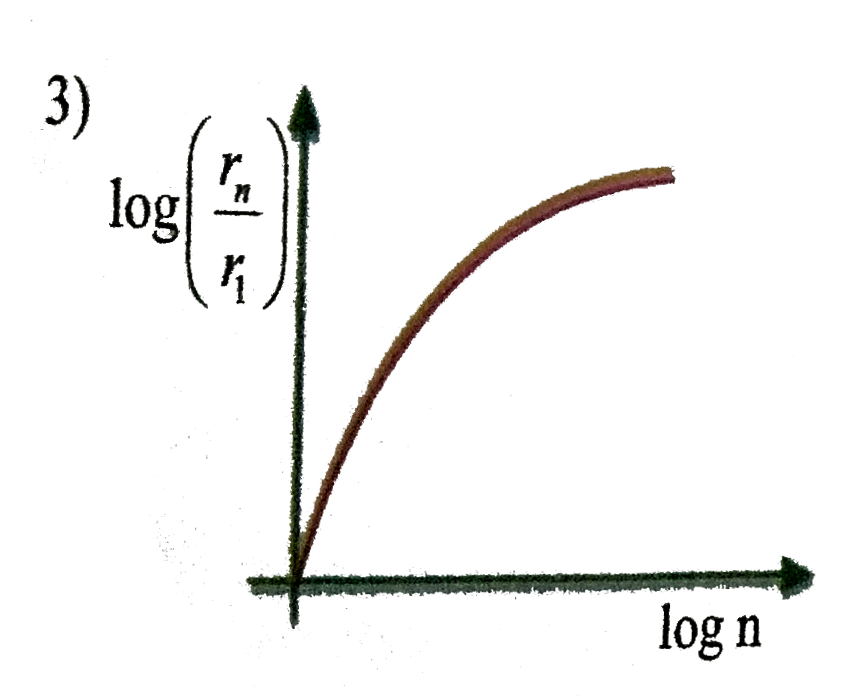 D
D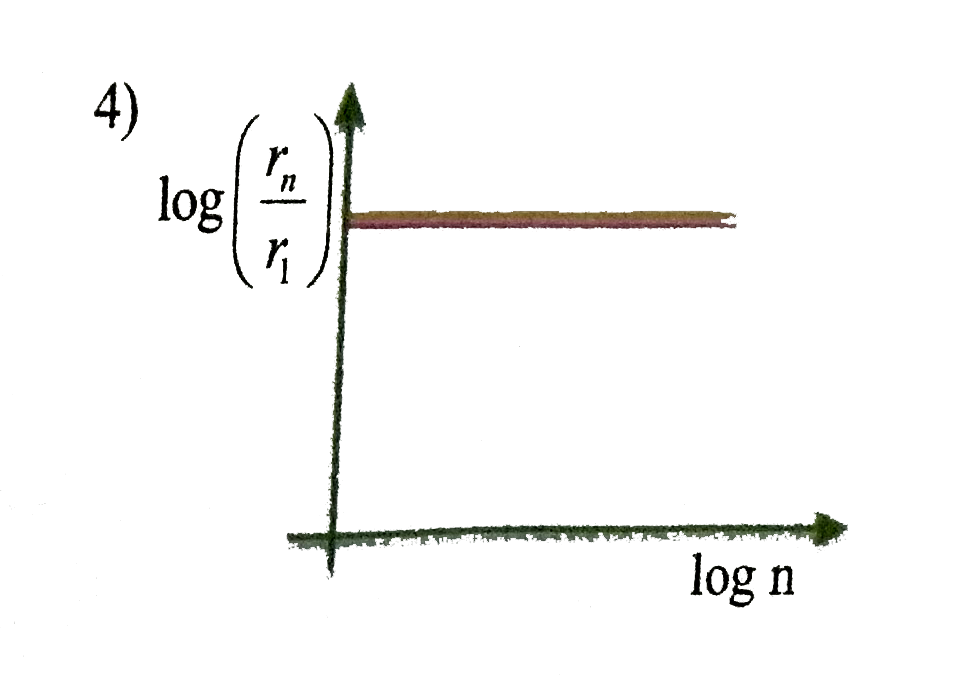
Time period of revolution of an electron in nth orbit in a hydrogen like atom is given by T=T0naZb,Z=atomic number
AT0=1.5×10−16s,a=3BT0=6.6×1015s,a=3CT0=1.51×10−16s,b=3DT0=6.6×1015s,b=3
Calculate the ratio of the radius of 1st orbit of H atom to thatof4thorbit.
Hint :rn∝(n)2
View SolutionThe period of f(x)=sin(πxn−1)+cos(πxn),n∈Z,n>2, is
View SolutionThe energy of an electron in the nth Bohr orbit of hydrogen atom is
View SolutionThe period of f(x)=sin(πxn−1)+cos(πxn),n∈Z,n>2, is
View SolutionIf n∈Z, then 2n(1+i)2n+(1+i)2n2n is equal to
View Solution

