Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals
√PQ.RS
PQ+RS2
2PQ.RSPQ+RS
√PQ2+RS22
The correct Answer is:A
Step by step video & text solution for Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Let PQ and RS be tangent at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQ×RS .
View SolutionLet PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. PS and RQ intersect at a point X on the circumference of the circle. If PQ = 9 and RS = 4, then the diameter of the circle is :
View Solution
Knowledge Check
If the sum of the circumferences of two circles with radii R1andR2 is equal to the circumference of a circle of radius R, then
AR1+R2=RBR1+R2>RCR1+R2<RDR21+R22<RIf the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then
AR1+R2=RBR1+R2>RCR1+R2<RDNothing definite can be said about the relation among R1,R2 and R.The tangents are drawn at the extremities of diameter AB of a circle with centre P. If a tangent to the circle at the point C Intersects the other two tangents at Q and R, then the measure of the ∠QPR is
A45∘B60∘C90∘D180∘
Write expression for circumference of a circle of radius 'r'
View SolutionIn the following figure,PQ is the diameter of the circle with radius 5 cm. if AT is the tangent and equal to the radius of the circle, then find the lenth of AR.
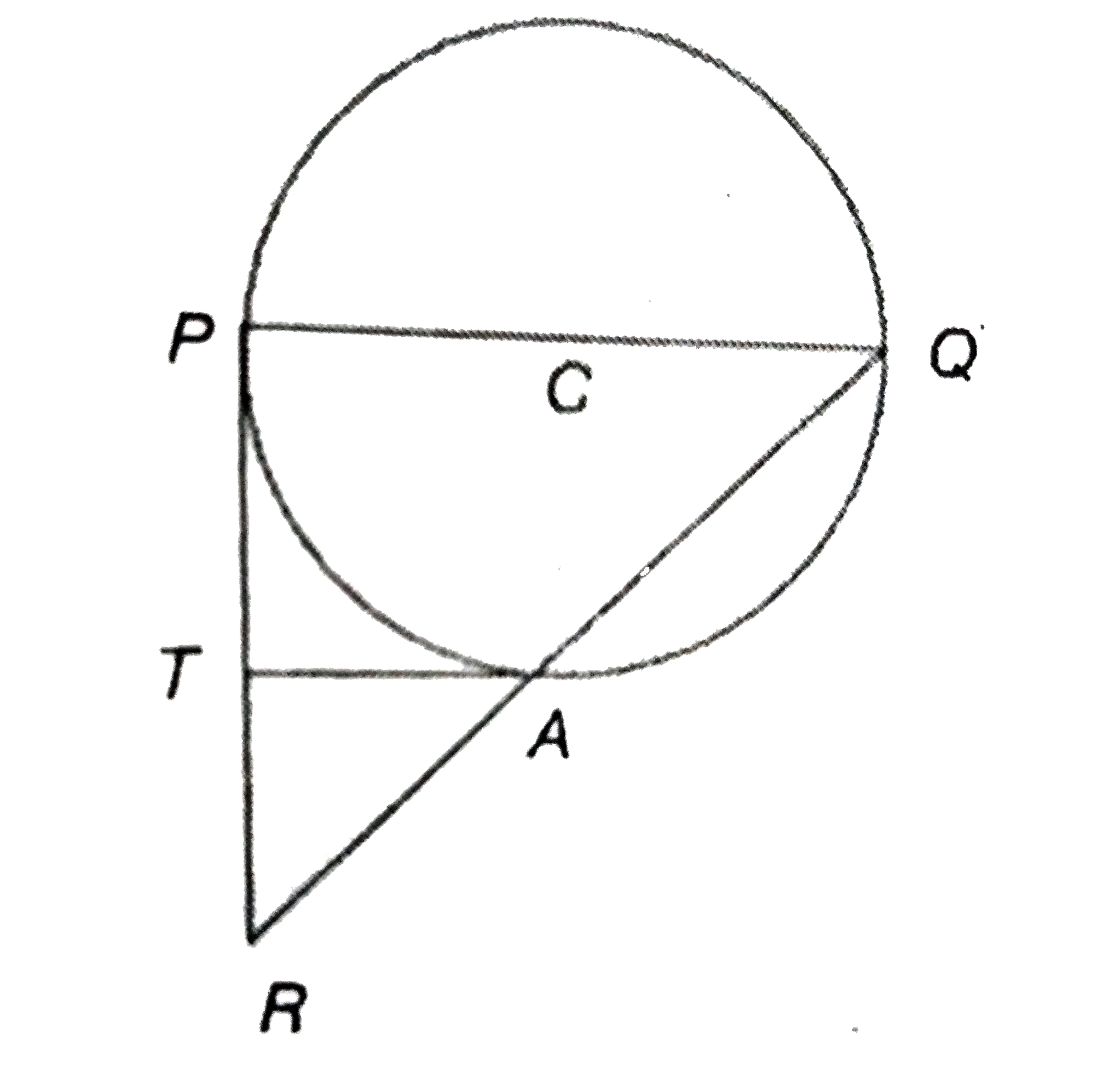
View SolutionTangents are drawn at extremities AB of a diameter of a circle centred at P. If tangents drawn at a point C on the circle meet the other two tangents respectively at Q and R then measure of ∠QPR is
View SolutionIf the area of a circle is A, radius of the circle is r and circumference of it is C, then
View SolutionIf the area of a circle is A, radius of the circle is r and circumference of it is C, then
View Solution