A block of mass m slips down an inclined plane as shown in the figure. When it reaches the bottom it presses the spring by a length (spring length ⟨h and spring constant = K)-
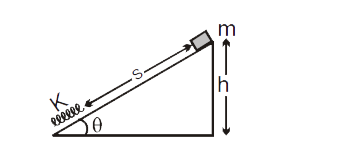
(2mgh/K)1/2
(mgh/K)1/2
(2gh/mK)1/2
(gh/mK)1/2
The correct Answer is:A
Step by step video, text & image solution for A block of mass m slips down an inclined plane as shown in the figure. When it reaches the bottom it presses the spring by a length (spring length <<h and spring constant = K)- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:Exercise - 2
Explore 30 Videos
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:Exercise - 3 Section-A
Explore 25 Videos
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:QUESTIONS FOR PRACTICE
Explore 25 Videos
- WAVESBook:MOTIONChapter:WAVESExercise:EXERCISE -4 (Level -II) (previous year JEE Advanced)
Explore 10 Videos
Similar Questions
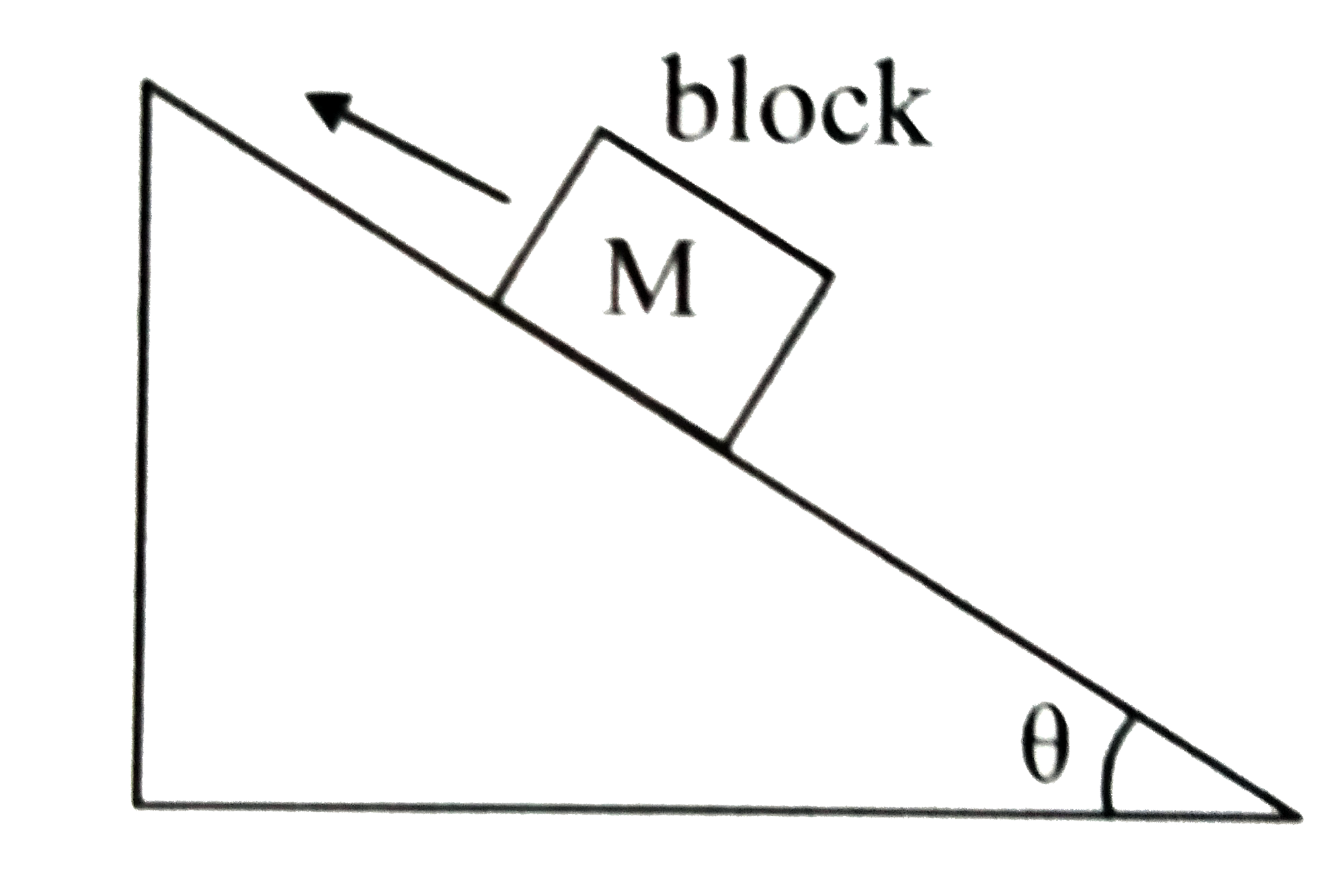
A block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is θ the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?
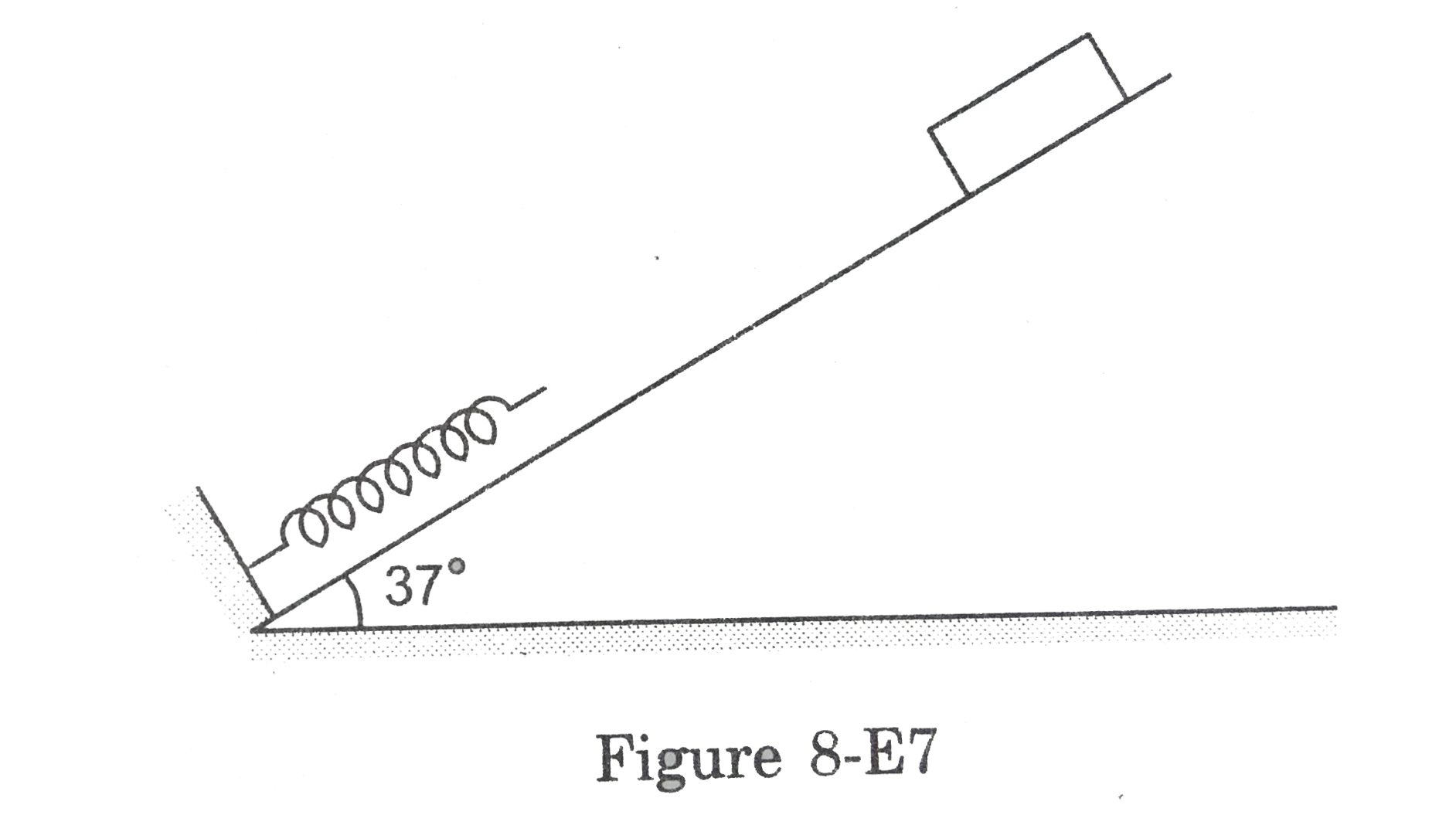
View SolutionFigure shows a spring fixed at the bottom end of an incline of inclination 370. A small block of mass 2 kg starts slipping down the incline from a point 4.8 m away from the spring. The block compresses the spring by 20 cm, stops momentarily and then rebounds through a distance of 1 m up the incline. Find a. the frictioin coefficient between the plane and the block and b. the spring constant of the spring. Take g=10ms2.
View Solution
Knowledge Check
block of mass m slips down an inclined plane as shown in the figure. When it reaches the bottom it presses the spring by a length (spring length ltlth and spring constant = K) - (A) (2mgh/K)1/2
 A(2mgh/K)1/2B(mgh/K)1/2C(2gh/mK)1/2D(gh//mK)^(1//2)
A(2mgh/K)1/2B(mgh/K)1/2C(2gh/mK)1/2D(gh//mK)^(1//2)A block of mass m is attached to the two springs in vertical plane as shown in the figure - 3.95. If initially both the springs are at their natural lengths then velocity of the block is maximum at displacement x given as
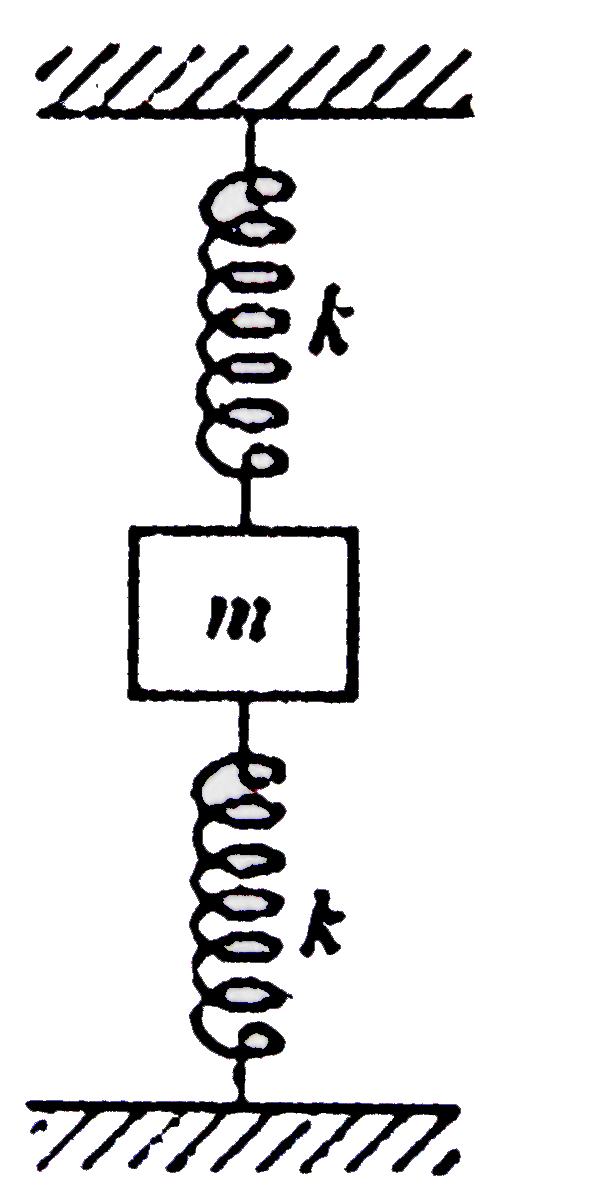 Ax=mg2kBx=mgkCx=mg4kDx=3mg2k
Ax=mg2kBx=mgkCx=mg4kDx=3mg2kA block of mass M slides down a rough inclined surface of inclination θ and reaches the bottom at speed at 'v' . However , if it slides down a smooth inclined surface of same length and same inclination , it reaches the bottom with the speed kv. Coefficient of friction between the block and the rough incline is :
Asinθ(k2−1)B(k2−1k2)tanθC(k2+1k2)cosθDk2−1k2
A system consists of block A and B each of mass m connected by a light spring as shown in the figure with block B in contact with a wall. The block A compresses the spring by 3mg/k from natural length of spring and then released from rest. Neglect friction anywhere.
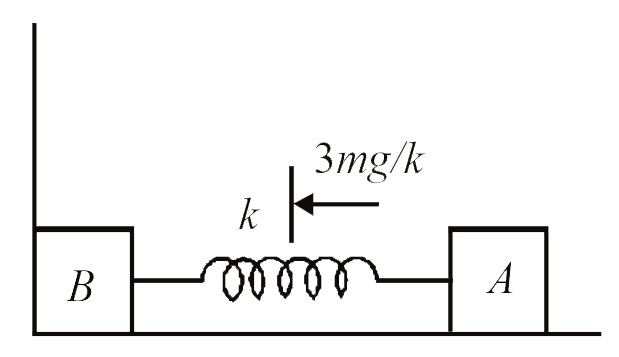
Maximum extension in the spring after system loses contact with wall
View SolutionA body of mass 5 kg is suspended by a spring balance on an inclined plane as shown in figure. The spring balance measure
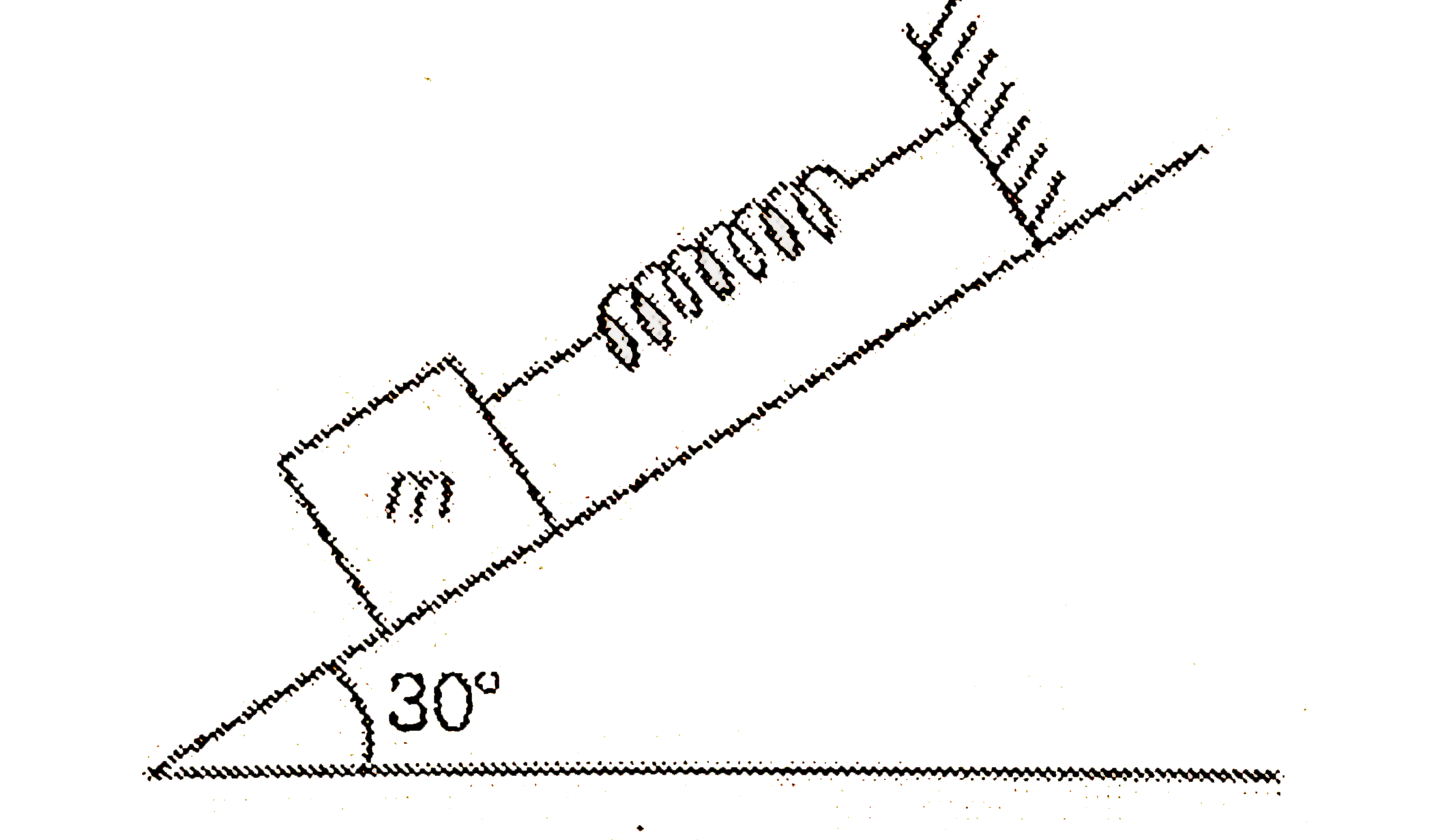
View SolutionA body of mass 5 kg is suspended by a spring balance on an inclined plane as shown in figure. The spring balance measure

View SolutionA block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
View SolutionA block of mass M is kept on a smooth surface and touches the two springs as shown in the figure but not attached to the springs. Initially springs are in their natural length. Now, the block is shifted (l0/2) from the given position in such a way that it compresses a spring and released. The time - period of oscillation of mass will be

View Solution

