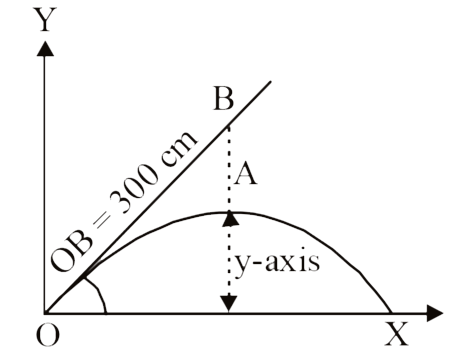
A ball 'A' is projected from origin with an initial velocity v0 = 700 cm/sec in a direction 37∘ above the horizontal as shown in fig .Another ball 'B' 300 cm from origin on a line 37∘ above the horizontal is released from rest at the instant A starts. How far will B have fallen when it is hit by A ?
9cm
90cm
0.9cm
900cm
Let the ball B hits the ball A after t sec The X-component of velocity of A is v0cos37∘=700cos37∘ The X-compoment of position of B is 300 cos37∘ The collision will take place when the X-coordinate of A is the same as that of B. As the collision takes place at a time t, hence 700cos37∘×t=300cos37∘ort=(300/700)=(3/7)sec In this time the ball B has fallen through a distance y =–1/2 gt2 (Free fall of body B) =–1/2×980×(3/7)2=–90cm Hence the ball B falls a distance 90 cm
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - PROJECTILE MOTIONEXERCISE - EXERCISE-139videos
PROJECTILE MOTION
- BOOK - MOTIONCHAPTER - PROJECTILE MOTIONEXERCISE - EXERCISE-222videos
PROJECTILE MOTION
- BOOK - MOTIONCHAPTER - PHOTOELECTRIC EFFECT EXERCISE - EXERCISE -3 (PREVIOUS YEAR PROBLEMS (JEE MAIN))12videos
PHOTOELECTRIC EFFECT
- BOOK - MOTIONCHAPTER - RADIOACTIVITY & NUCLEAR PHYSICSEXERCISE - Exercise-381videos
RADIOACTIVITY & NUCLEAR PHYSICS
Similar Questions
A ball is projeced from O with an initial velocity 700 cm/ s in a direction 37∘ above the horizontal. A ball B, 500 cm away from O on the line of the initial velocity of A, is released from rest at the instant A is projected. The height through which B falls, before it is hit by A and the direction of the velocity A at the time of impact will respectively be [Given g=10m/s2,sin37∘=0.6andcos37∘=0.8]
View SolutionA cannon ball is thrown with an initial velocity of 40ms at an angle of 53∘ above the horizontal from ground.After some time,the ball is seen to travel at an angle of 37∘ below horizontal.Find the time elapsed (in second) till then.
View Solution
Knowledge Check
- Question 1 - Select One
A ball is projected from a point A with some velocity at an angle 30∘ with the horizontal as shown in (Fig. 5.204). Consider a target at point B. The ball will hit the target if it thrown with a velocity v0 equal to.
 .A5ms−1B6ms−1C7ms−1DNone of these
.A5ms−1B6ms−1C7ms−1DNone of these - Question 2 - Select One
A ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
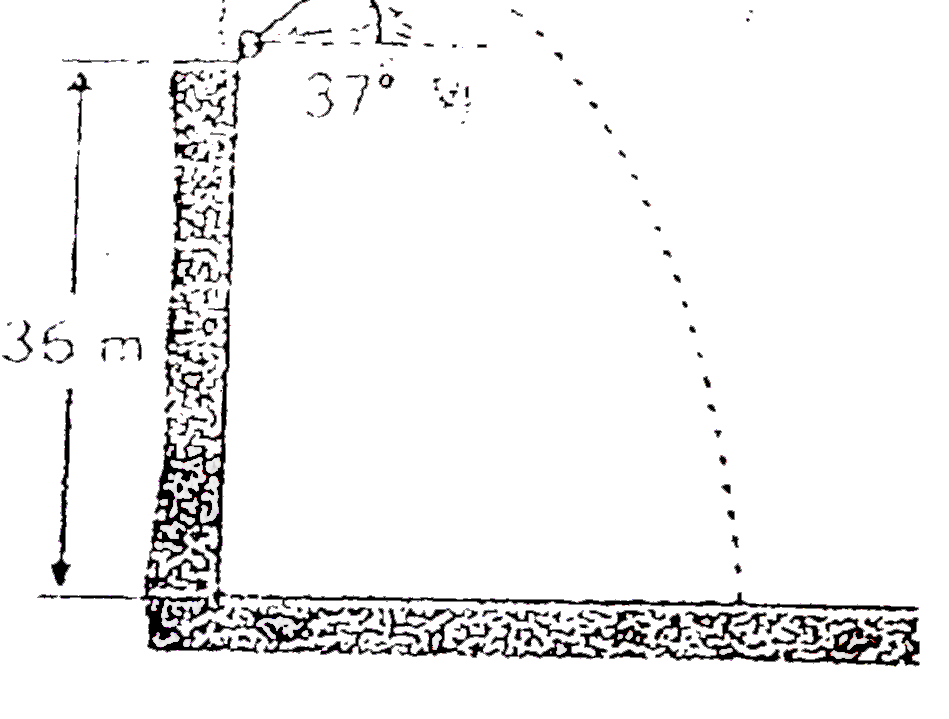 : A12mB18mC24mD30m
: A12mB18mC24mD30m - Question 3 - Select One
A paricle is projected from a point with initial speed of 10m/sec at an angle of 37∘ with the horizontal. At the same instant a fly starts on the same path of particle with constant speed of 10m/s Then :
Atime taken by fly to complete whole path is less then time taken by particleBacceleration of fly is zeroCaverage velocity of both are same for whole journeyDNone of these
A footballer throws a ball from a height of 2.00m above the ground with an initial velocity of 20.0m/s at an angle of 30∘ above the horizontal (a) How long does the ball take to cross the goal line 32.0m from the point of release?(b) What is the ball's height above the ground as it crosses the goal line?
View SolutionA ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View SolutionA ball is projected directly upward with an initial speed v0. Bounces elastically from a roof inclined at an angle 45∘ as shown in figure and then it strikes a table at a horizontal distance 2D from its starting point. Find v0.
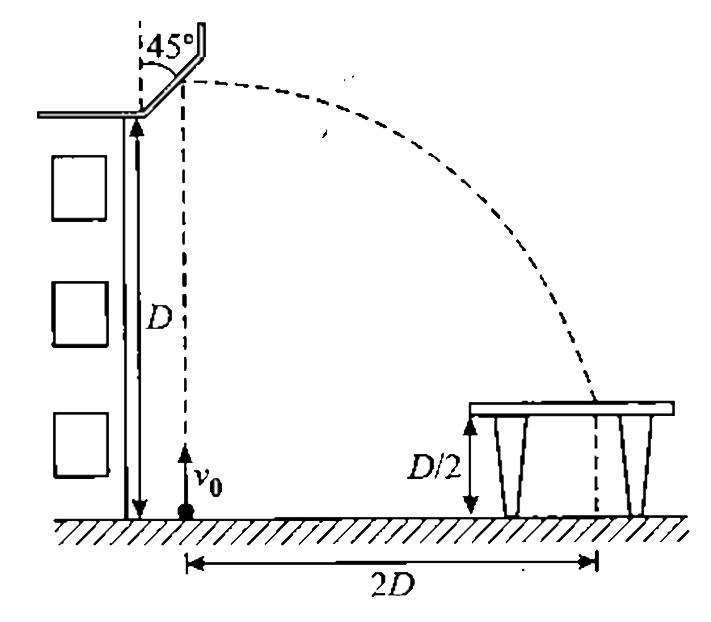 View Solution
View SolutionA ball A is projected with speed 20m/s at an angle of 30∘ with the horizontal from the ground. Another ball B is released simultaneously from a point on the vertical line along the maximum height of the projectile. Both the balls collide at the maximum height of the first ball. The initial height of ball B is
View SolutionA cricketer hits a ball with a velocity 25m/s at 60∘ above the horizontal. How far above the ground it passes over a fielder 50 m from the bat (assume the ball is struck very close to the ground)
View Solution

