A ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
The correct Answer is:8 m
To solve the problem of finding the height of the tower from which a ball is thrown, we can break down the motion into horizontal and vertical components. Here’s a step-by-step solution:
Step 1: Resolve the initial velocity into horizontal and vertical components.
The ball is thrown with an initial velocity u=10m/s at an angle of 37∘ above the horizontal.
- Horizontal component ux=ucos(37∘)
- Vertical component uy=usin(37∘)
Using the values:
- cos(37∘)=45
- sin(37∘)=35
Calculating the components:
ux=10⋅45=8m/s
uy=10⋅35=6m/s
Step 2: Determine the time of flight.
The horizontal distance covered by the ball is given as d=16m. The time t taken to cover this distance can be calculated using the formula:
d=ux⋅t
Rearranging gives:
t=dux=168=2s
Step 3: Calculate the height of the tower.
Using the vertical motion equation to find the height h:
h=uyt−12gt2
Substituting the known values:
- uy=6m/s
- g=10m/s2
- t=2s
Calculating:
h=6⋅2−12⋅10⋅(22)
h=12−12⋅10⋅4
h=12−20
h=−8m
Since height cannot be negative, we interpret this as the height of the tower being 8m (the negative sign indicates that the displacement is downward).
Final Answer:
The height of the tower is 8m.
---
The ball is thrown with an initial velocity u=10m/s at an angle of 37∘ above the horizontal.
- Vertical component uy=usin(37∘)
- cos(37∘)=45
- sin(37∘)=35
ux=10⋅45=8m/s
uy=10⋅35=6m/s
The horizontal distance covered by the ball is given as d=16m. The time t taken to cover this distance can be calculated using the formula:
d=ux⋅t
Rearranging gives:
t=dux=168=2s
Using the vertical motion equation to find the height h:
h=uyt−12gt2
Substituting the known values:
- uy=6m/s
- g=10m/s2
- t=2s
h=6⋅2−12⋅10⋅(22)
h=12−12⋅10⋅4
h=12−20
h=−8m
The height of the tower is 8m.
Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-1)
30 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
15 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A ball is thrown from the top of a tower with an initial velocity of 10 m//s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
View SolutionA stone is thrown up from the top of a tower 20,m with a velocity of 24m/s a tan elevation of 30∘ above the horizontal. Find the horizontal distance from the foot of the tower to the point at which the stone hits the ground. Take g=10m/s2
View Solution
Knowledge Check
A ball is thrown from the top of tower with an initial velocity of 10ms−1 at an angle of 30∘ with the horizontal. If it hits the ground of a distance of 17.3m from the back of the tower, the height of the tower is (Takeg=10ms−2)
A5mB20mC15mD10mA ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
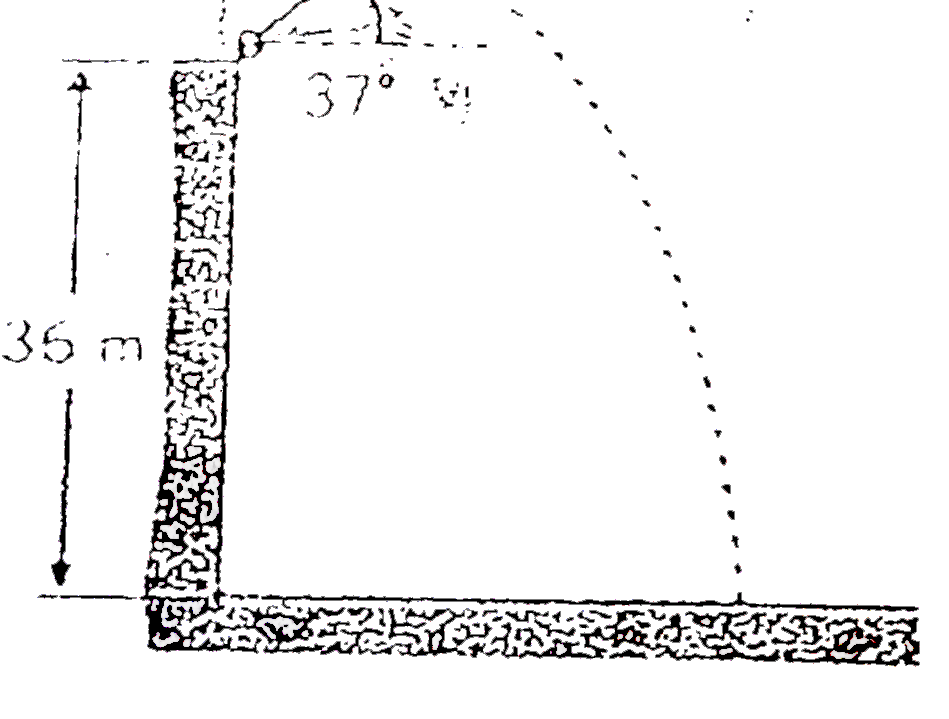 : A12mB18mC24mD30m
: A12mB18mC24mD30mA ball is thrown upwards from the top of a tower 40m high with a velocity of 10m/s. Find the time when it strikes the ground. Take g=10m/s2.
A4sB−28sC12sD−2s
A ball is thrown from the top of a tower of 61m high with a velocity 24.4ms−1 at an elevation of 30∘ above the horizontal. What is the distance from the foot of the tower to the point where the ball hits the ground?
View SolutionA tower of height 5m and a flagstaff on top of the tower subtend equal angles at a point on the ground, distance 13m from the base of the tower. The height of the flagstaff is
View SolutionA pebbel is thrown horizantally from the top of a 20 m high tower with an initial velocity of 10m/s.The air drag is negligible . The speed of the peble when it is at the same distance from top as well as base of the tower (g=10m/s2)
View SolutionA stone is thrown from the top of a tower at an angle of 30∘ above the horizontal level with a velocity of 40 m/s. it strikes the ground after 5 second from the time of projection then the height of the tower is
View SolutionA ball is thrown from the top of a 60m high tower with velocity 20√2m/s at 45∘ elevation of path at highest point. (g=10m/s2)
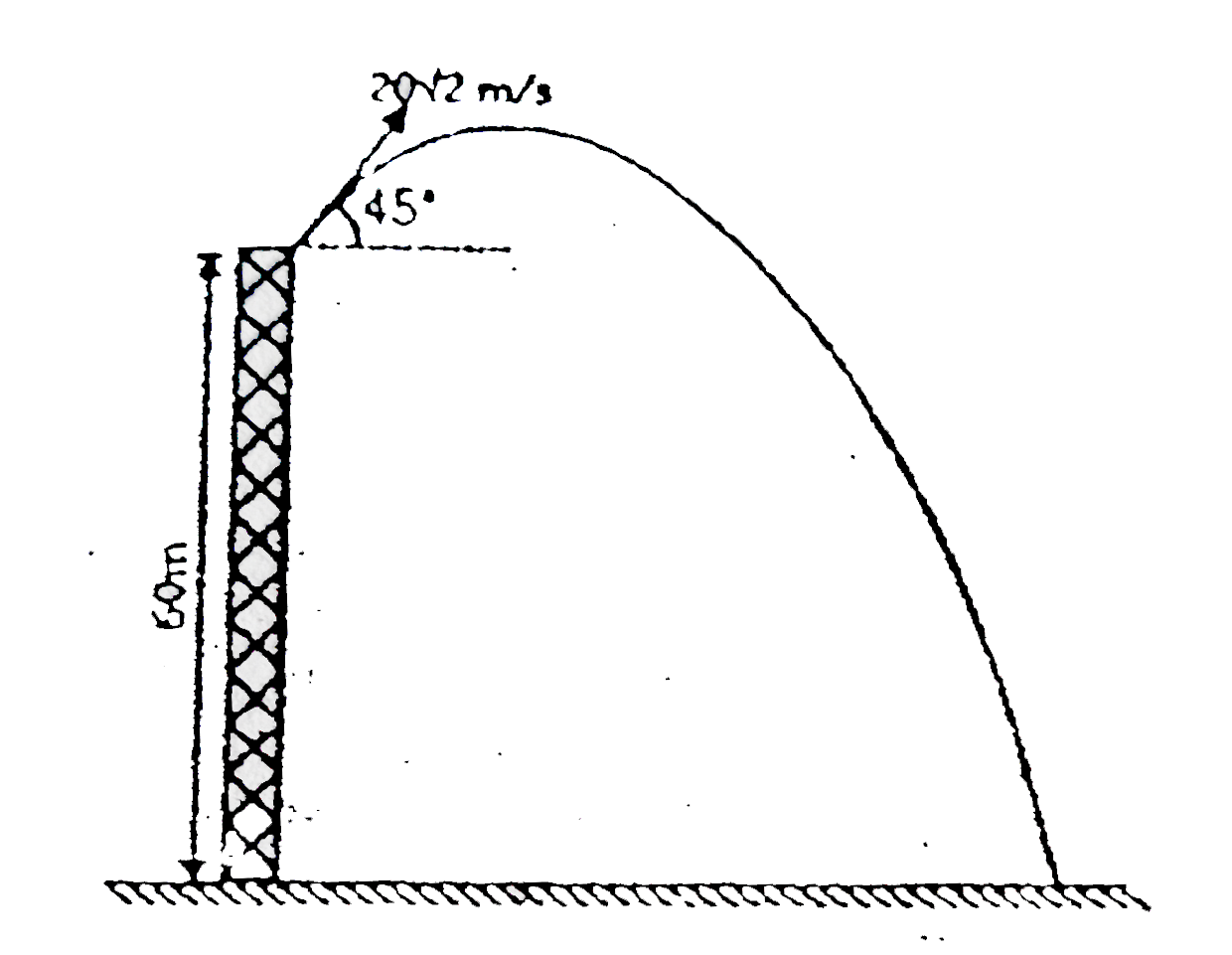
View Solution
