If C is the midpoint of the point A(−3,−4)andB(−5,6), then AC =
5
√26
√61
8
The correct Answer is:B
To find the length of AC, where C is the midpoint of points A and B, we can follow these steps:
Step 1: Identify the coordinates of points A and B
The coordinates of point A are given as A(-3, -4) and the coordinates of point B are given as B(-5, 6).
Step 2: Use the midpoint formula to find the coordinates of point C
The midpoint C of two points A(x1, y1) and B(x2, y2) is calculated using the formula:
C(x1+x22,y1+y22)
Substituting the coordinates of A and B:
C(−3+(−5)2,−4+62)=C(−82,22)=C(−4,1)
Step 3: Calculate the length of segment AB using the distance formula
The distance between two points A(x1, y1) and B(x2, y2) is given by the formula:
AB=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of A and B:
AB=√(−5−(−3))2+(6−(−4))2=√(−5+3)2+(6+4)2
This simplifies to:
AB=√(−2)2+(10)2=√4+100=√104
Step 4: Simplify the distance AB
We can simplify √104:
√104=√4×26=√4×√26=2√26
Step 5: Find the length of AC
Since C is the midpoint of AB, the length of AC is half of AB:
AC=AB2=2√262=√26
Final Answer
Thus, the length of AC is √26.
---
The coordinates of point A are given as A(-3, -4) and the coordinates of point B are given as B(-5, 6).
The midpoint C of two points A(x1, y1) and B(x2, y2) is calculated using the formula:
C(x1+x22,y1+y22)
Substituting the coordinates of A and B:
C(−3+(−5)2,−4+62)=C(−82,22)=C(−4,1)
The distance between two points A(x1, y1) and B(x2, y2) is given by the formula:
AB=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of A and B:
AB=√(−5−(−3))2+(6−(−4))2=√(−5+3)2+(6+4)2
This simplifies to:
AB=√(−2)2+(10)2=√4+100=√104
We can simplify √104:
√104=√4×26=√4×√26=2√26
Since C is the midpoint of AB, the length of AC is half of AB:
AC=AB2=2√262=√26
Thus, the length of AC is √26.
Similar Questions
Knowledge Check
Column AC is the midpoint of points A(-3, -4) and the originColumn BSlope of ACSlope of BC
AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
The coordinates of the point P dividing the line segment joining the points A(1, 3) and B(4, 6) in the ratio 2 :1 are (2, 4) (b) (3, 5) (c) (4, 2) (d) (5, 3)
View SolutionP and Q are points on the line joining A(−2,5) and B(3,1) such that AP=PQ=QB . Then the distance of the midpoint of PQ from the origin is (a)3 (b) √372 (c) 4 (d) 3.5
View SolutionPlot the points A(4,2),B(−5,3),C(−4,−5)andD(5,−2).
View SolutionA, B, C, and D all lie on a number line. C is the midpoint of ¯¯¯¯¯¯AB and D is the midpoint of ¯¯¯¯¯¯AC.
Quantity AQuantity BThe ratio of ¯¯¯¯¯¯AD to ¯¯¯¯¯¯CBThe ratio of ¯¯¯¯¯¯AC to ¯¯¯¯¯¯AB
View SolutionIf A and B are the points (−3,4) and (3,−4) respectively then the co-ordinates of the point C on AB produced such that AC=3BC are
(A) (0,0)
(B) (−6,8)
(C) (6,−8)
(D) (−6,−8)
View SolutionName the type of triangle formed by the points A (-5,6) , B (-4,-2) and C (7,5).
View SolutionA parallelogram ABCD has P the mid-point of DC and Q a midpoint of AC such that CQ=14AC.PQ produced meets BC at R. Prove that:
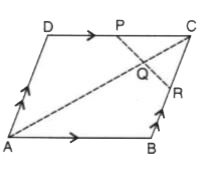
R is the mid-point of BC
View Solution
