If xaxb(xc)d=x2 for all x≠0, which of the following must be true?
a+b−cd=2
a+bcd=2
ab−cd=2
ab−cd=2
The correct Answer is:A
To solve the equation xa⋅xb(xc)d=x2 for all x≠0, we can follow these steps:
Step 1: Simplify the left-hand side
We start by simplifying the left-hand side of the equation. We can use the properties of exponents to combine the terms in the numerator and the denominator.
xa⋅xb(xc)d=xa+bxcd
Step 2: Apply the quotient rule of exponents
Next, we apply the quotient rule of exponents, which states that xmxn=xm−n.
xa+bxcd=x(a+b)−cd
Step 3: Set the exponents equal
Now, we set the exponent from the left-hand side equal to the exponent on the right-hand side of the equation, which is 2.
(a+b)−cd=2
Step 4: Rearrange the equation
We can rearrange the equation to express a relationship between a, b, c, and d.
a+b−cd=2⟹a+b=cd+2
Conclusion
Thus, the relationship that must be true for the equation to hold for all x≠0 is:
a+b−cd=2
We start by simplifying the left-hand side of the equation. We can use the properties of exponents to combine the terms in the numerator and the denominator.
Next, we apply the quotient rule of exponents, which states that xmxn=xm−n.
Now, we set the exponent from the left-hand side equal to the exponent on the right-hand side of the equation, which is 2.
We can rearrange the equation to express a relationship between a, b, c, and d.
Thus, the relationship that must be true for the equation to hold for all x≠0 is:
Similar Questions
Knowledge Check
If x+y=90∘, which of the following must be true?
Acosx=cosyBsin x=-sin yCtan x=cot yDsin x+cos y=1If f(x)=x3, which of the following must be true ?
Af(−x)=f(x)Bf(−x)=−f(−x)Cf(−x)=−f(x)Df(x)=−f(x)If 4x−12≥x+9, which of the following must be true ?
Ax>6Bx<7Cx≥7Dx>8
If x is integer and x2 is even, which of the following must be true?
View SolutionIf f(x)≥0 and g(x)≥0 for all real x, which of the following statements must be true ?
I. f(x)+g(x)≥0
II. f(x)−g(x)≥0
III. f(x)g(x)≥0
View SolutionIf x=a+2andb=x+1, then which of the following must be false?
View Solution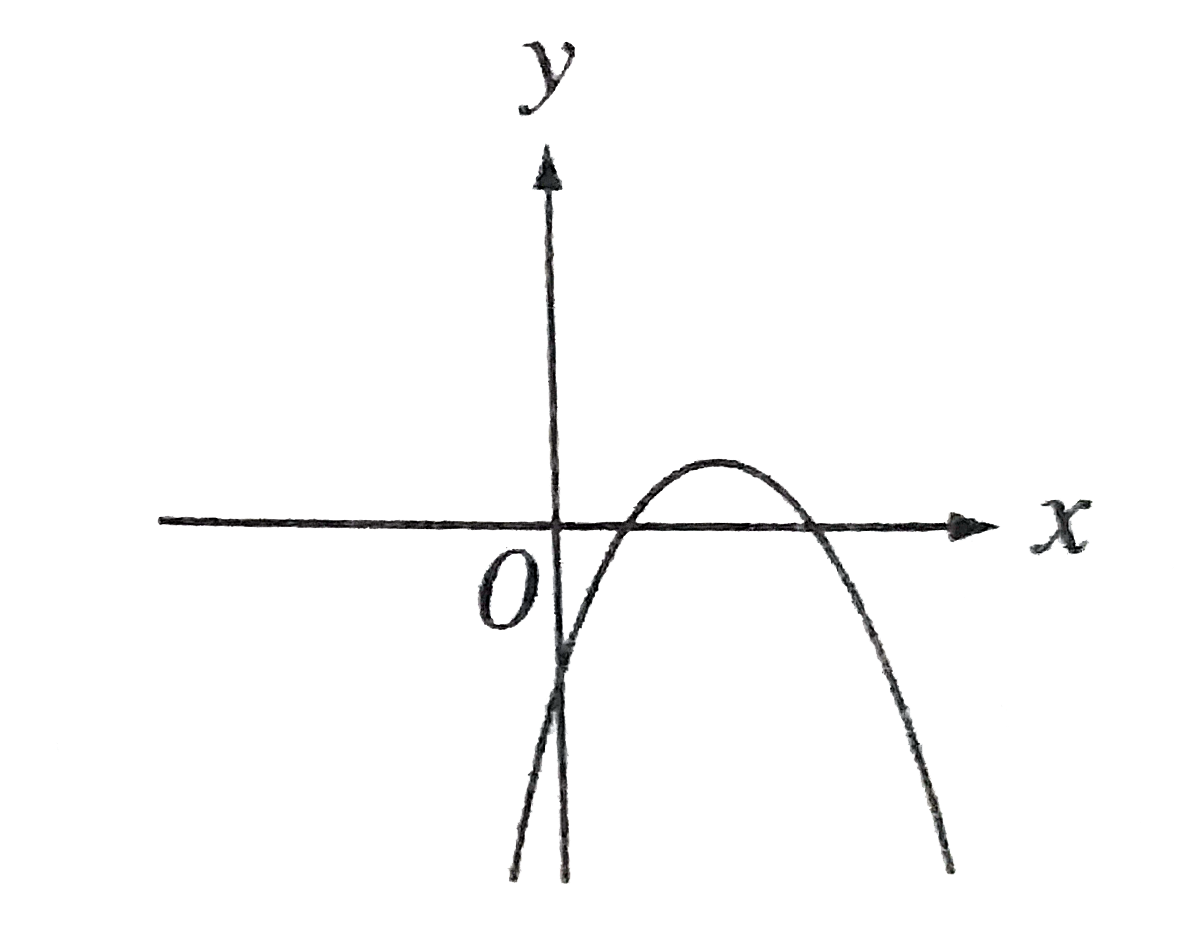
The graph of y=g(x) is shown in the figure above. If g(x)=ax2+bx+c for constants a,b and c and if abc≠0, then which of the following must be true?
View Solution18x4+27x3−36x29x2 If x≠0, which of the following is equivalent to the expression above ?
View Solution

