If x is integer and x2 is even, which of the following must be true?
x is even
x is odd
x3 is odd
x3 is even
The correct Answer is:A
To solve the problem, we need to determine what must be true if x is an integer and x2 is even.
1. Understanding the Condition: We start with the condition that x2 is even. Recall that a number is even if it can be expressed as 2k, where k is an integer.
2. Analyzing x2: If x2 is even, we can use the property of squares. The square of an integer is even if and only if the integer itself is even.
3. Using Contradiction: Let's assume x is odd. An odd integer can be expressed in the form x=2k+1 for some integer k. Squaring this gives:
x2=(2k+1)2=4k2+4k+1=2(2k2+2k)+1
This shows that x2 is odd, which contradicts our initial condition that x2 is even.
4. Conclusion: Since assuming x is odd leads to a contradiction, we conclude that x must be even.
5. Final Statement: Therefore, if x2 is even, it must be true that x is even.
x2=(2k+1)2=4k2+4k+1=2(2k2+2k)+1
This shows that x2 is odd, which contradicts our initial condition that x2 is even.
Similar Questions
Knowledge Check
If x and y are positive integers and (2x +y) is even, which of the following must be even ?
Ax3+2xy2B3x2+2yC4x2+x+y2D5x2+x+y3If x+y=90∘, which of the following must be true?
Acosx=cosyBsin x=-sin yCtan x=cot yDsin x+cos y=1If f(x)=x3, which of the following must be true ?
Af(−x)=f(x)Bf(−x)=−f(−x)Cf(−x)=−f(x)Df(x)=−f(x)
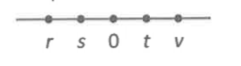
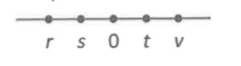
Which of the following MUST be true?
v+s>t+r
View SolutionIf a,b,andc are consecutive integers and a < b < c, which one of the following must be true?
View SolutionIf −3x+6≥18, which of the following must be true?
View SolutionIf ab>0, then which one of the following must be true?
View SolutionFrom the figure, which one of the following must be true?
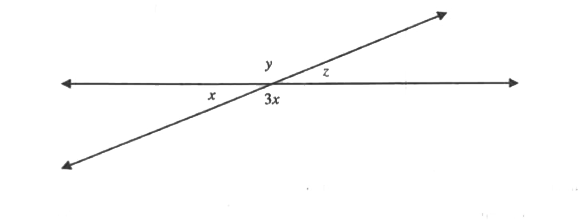
View Solution