For which of the following lists of 5 numbers is the average (arithmetic mean) greatest than the median?
3, 3, 5, 8, 8
2, 3, 5, 6, 7
3, 3, 5, 7, 7
3, 4, 5, 6, 7
The correct Answer is:A
To determine which list of 5 numbers has an average (arithmetic mean) greater than the median, we will follow these steps:
Step 1: Identify the Lists
We have four lists of numbers:
- Option A: 3, 3, 5, 8, 8
- Option B: 2, 3, 5, 6, 7
- Option C: 3, 3, 5, 7, 7
- Option D: 3, 4, 5, 6, 7
Step 2: Calculate the Median
For a list of 5 numbers, the median is the third number when the numbers are arranged in ascending order.
- Option A: The numbers are 3, 3, 5, 8, 8. The median is 5 (the third number).
- Option B: The numbers are 2, 3, 5, 6, 7. The median is 5 (the third number).
- Option C: The numbers are 3, 3, 5, 7, 7. The median is 5 (the third number).
- Option D: The numbers are 3, 4, 5, 6, 7. The median is 5 (the third number).
Step 3: Calculate the Average (Mean)
The average is calculated by summing all the numbers and dividing by the total count (which is 5 in this case).
- Option A:
Mean=3+3+5+8+85=275=5.4
- Option B:
Mean=2+3+5+6+75=235=4.6
- Option C:
Mean=3+3+5+7+75=255=5
- Option D:
Mean=3+4+5+6+75=255=5
Step 4: Compare Mean and Median
Now we compare the mean and median for each option:
- Option A: Mean = 5.4, Median = 5 (Mean > Median)
- Option B: Mean = 4.6, Median = 5 (Mean < Median)
- Option C: Mean = 5, Median = 5 (Mean = Median)
- Option D: Mean = 5, Median = 5 (Mean = Median)
Conclusion
The only option where the average (mean) is greater than the median is Option A: 3, 3, 5, 8, 8.
---
We have four lists of numbers:
- Option A: 3, 3, 5, 8, 8
- Option B: 2, 3, 5, 6, 7
- Option C: 3, 3, 5, 7, 7
- Option D: 3, 4, 5, 6, 7
For a list of 5 numbers, the median is the third number when the numbers are arranged in ascending order.
- Option B: The numbers are 2, 3, 5, 6, 7. The median is 5 (the third number).
- Option C: The numbers are 3, 3, 5, 7, 7. The median is 5 (the third number).
- Option D: The numbers are 3, 4, 5, 6, 7. The median is 5 (the third number).
The average is calculated by summing all the numbers and dividing by the total count (which is 5 in this case).
Mean=3+3+5+8+85=275=5.4
- Option B:
Mean=2+3+5+6+75=235=4.6
Mean=3+3+5+7+75=255=5
Mean=3+4+5+6+75=255=5
Now we compare the mean and median for each option:
- Option B: Mean = 4.6, Median = 5 (Mean < Median)
- Option C: Mean = 5, Median = 5 (Mean = Median)
- Option D: Mean = 5, Median = 5 (Mean = Median)
The only option where the average (mean) is greater than the median is Option A: 3, 3, 5, 8, 8.
Similar Questions
Knowledge Check
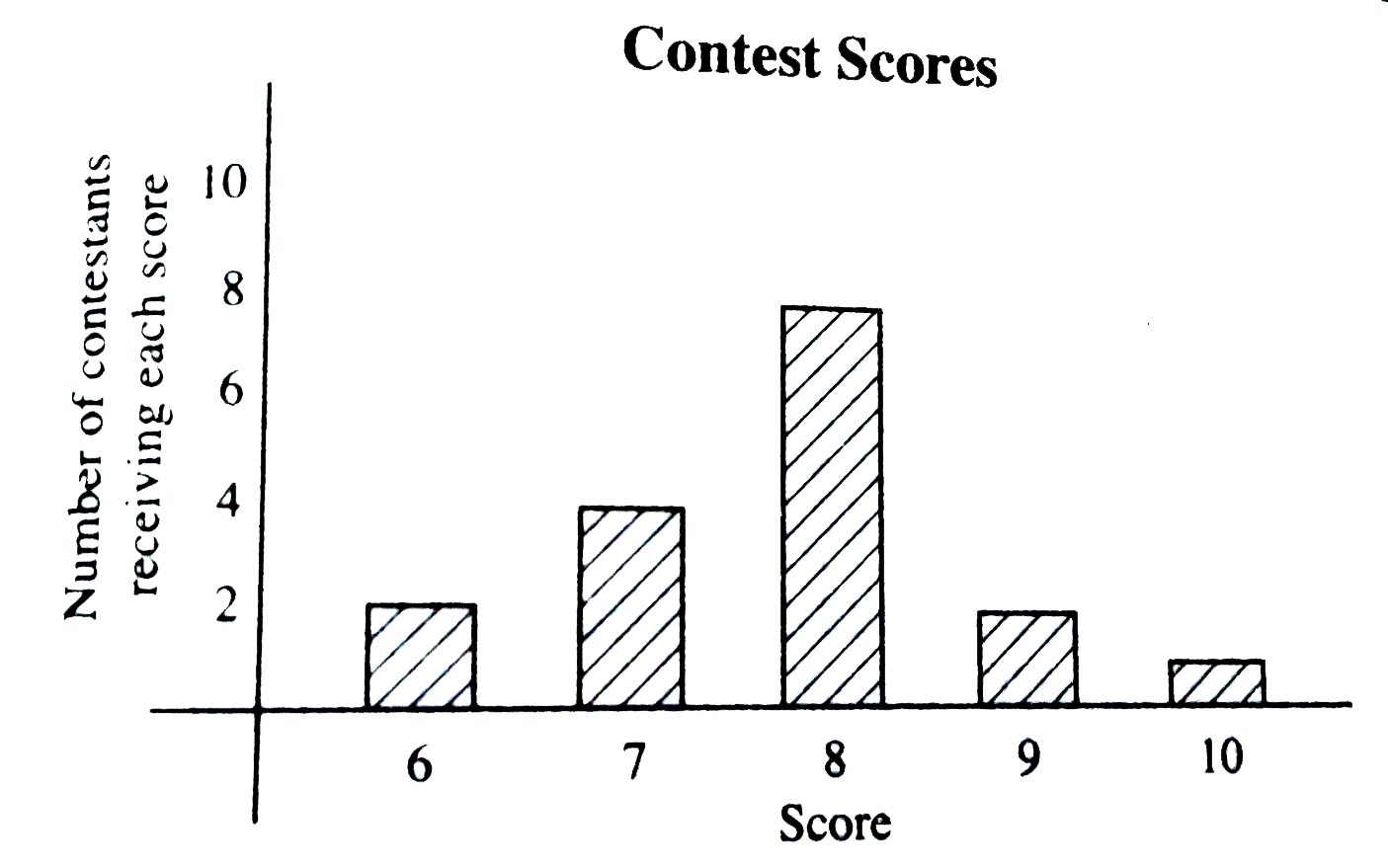
In a contest , each contestant could receive a score of 6,7,8,9, or 10. The bar graph above shows how many contestants received each score .
The score of 8 is described by which of the following measures ?
I.The average (arithmetic mean )
II.The median
III.The modeAI onlyBII onlyCIII onlyDII and III only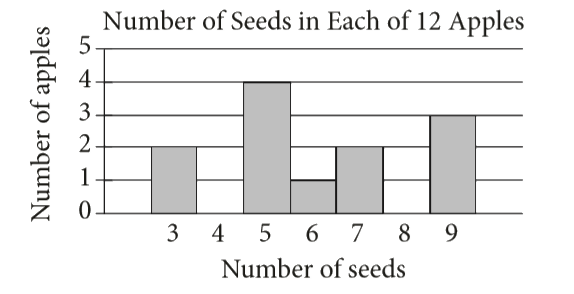
Based on the histogram above, of the following, which is closest to the average (arithmetic mean) number of seeds per apple?A4B5C6D7
Which of the following contains greatest number of oxygen atoms ? .
View SolutionFind two numbers whose arithmetic mean is 34 and the geometric mean is 16.
View SolutionFind two numbers whose arithmetic mean is 34 and the geometric mean is 16.
View SolutionFind two numbers whose arithmetic mean is 34 and the geometric mean is 16.
View SolutionWhich of the following contains the greatest number of atoms ?
View SolutionFind two number whose arithmetic mean is 34 and the geometric mean is 16 .
View Solution
