United Telephone charges a base rate of $10.00 for service, plus an additional charge of $0.25 per minute. Atlantic Call charges a base rate of $12.00 for service, plus an additional charge of $0.20 per minute. For what number of minutes would the bills for each telephone company be the same?
The correct Answer is:40 minutes
To solve the problem, we need to set up equations for the charges from both telephone companies and find the point at which they are equal.
1. Define Variables:
Let x be the number of minutes for which the bills of both companies are the same.
2. Set Up the Equation for United Telephone:
United Telephone charges a base rate of $10.00 plus $0.25 per minute. Therefore, the total charge CU for United Telephone can be expressed as:
CU=10+0.25x
3. Set Up the Equation for Atlantic Call:
Atlantic Call charges a base rate of $12.00 plus $0.20 per minute. Therefore, the total charge CA for Atlantic Call can be expressed as:
CA=12+0.20x
4. Set the Equations Equal to Each Other:
To find the number of minutes x where the charges are the same, we set CU equal to CA:
10+0.25x=12+0.20x
5. Rearrange the Equation:
To solve for x, first, we can move all terms involving x to one side and constant terms to the other side:
0.25x−0.20x=12−10
Simplifying this gives:
0.05x=2
6. Solve for x:
Now, divide both sides by 0.05 to isolate x:
x=20.05
Calculating this gives:
x=40
7. Conclusion:
The number of minutes for which the bills for each telephone company would be the same is 40 minutes.
Let x be the number of minutes for which the bills of both companies are the same.
United Telephone charges a base rate of $10.00 plus $0.25 per minute. Therefore, the total charge CU for United Telephone can be expressed as:
CU=10+0.25x
Atlantic Call charges a base rate of $12.00 plus $0.20 per minute. Therefore, the total charge CA for Atlantic Call can be expressed as:
CA=12+0.20x
To find the number of minutes x where the charges are the same, we set CU equal to CA:
10+0.25x=12+0.20x
To solve for x, first, we can move all terms involving x to one side and constant terms to the other side:
0.25x−0.20x=12−10
Simplifying this gives:
0.05x=2
Now, divide both sides by 0.05 to isolate x:
x=20.05
Calculating this gives:
x=40
The number of minutes for which the bills for each telephone company would be the same is 40 minutes.
Similar Questions
A mobile phone-based taxi service a base fee of $2 plus an amount per mile for the trip. Ariel is charged $16.94 for a ride that takes 14 minutes and travels 10 miles. Victoria is charged $11.30 for ride that take 10 minutes and travels 6 miles.
Q. What is the per-minute charge?View SolutionA mobile phone-based taxi service a base fee of $2 plus an amount per mile for the trip. Ariel is charged $16.94 for a ride that takes 14 minutes and travels 10 miles. Victoria is charged $11.30 for ride that take 10 minutes and travels 6 miles.
Q. What would be the carge for a ride that takes 8 minutes and travels 5 miles?View Solution
Knowledge Check
- Question 1 - Select One
Tamara has a cell phone that charges $0.07 per minute plus a monthly fee of $19.00. She budgets $29.50 per month for total cell phone expenses without taxes. What is the maximum number of minutes. Tamara could use her phone each month in order to stay withi her budget?
A150B271C421D682 - Question 2 - Select One
A long-distance telephone call costs $1.80 for the first 3 minutes and $0.40 for each additional minutes. If the charge for an x-minutes long distance call at this rate was $4.20, then x=
A7B8C9D10 - Question 3 - Select One
What garages each charge a fixed amount, plus an hourly rate, to service a car. The garage on Main street charged one customer $153 for a 2 hour service appointment, and it charged a second customer $315 for a 5 hour service appointment. The garage on 2nd Street charges $5 lee per hour than the garages on Main Street and $10 more for the fixed amount. How much would the garage on 2nd Street charges for a 3 hour service appointment?
A157B174C181D202
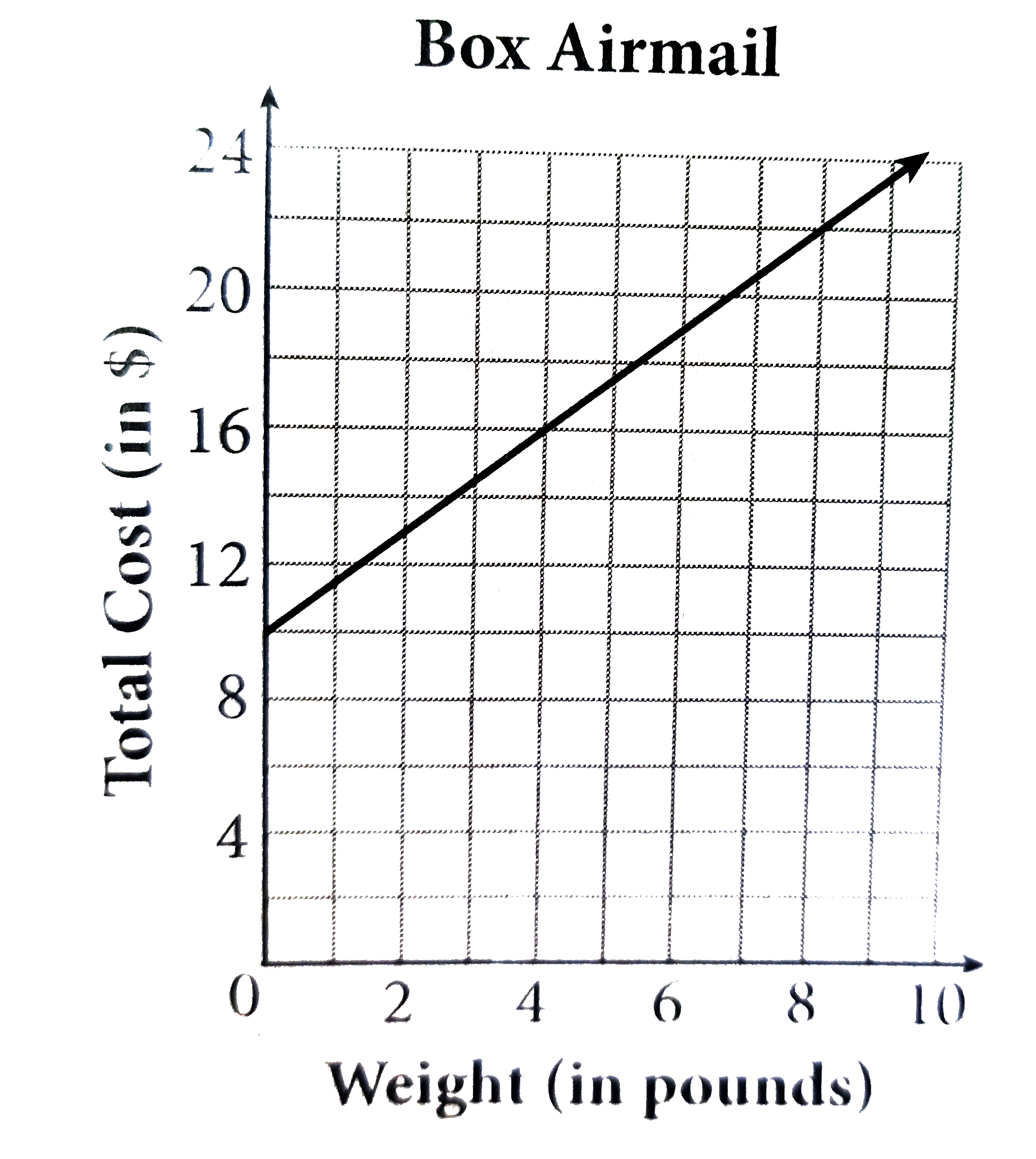
A freight airline charges a flat fee to airmil a box, plus an additional charge for each pound the box weights. The graph above shows the relationship between the weitht of the box and the total cost to airmail it. Based on the graph, how much would it cost in dollars to airmail a 40-pound boxView SolutionA text messaging plan charges a flat fee of $5 per month for up to 100 text messages sent plus $0.25 for each additional text message sent that month. Which of the following graphs represents the cost, y, of sending x texts in a month?
View SolutionAfter visiting Florida State University during spring break, Francisco rents a car for 2 days to travel around Florida. He has $255 to spend on car rental for the 2 days. Sea horse Car Rental charges $50 per day and $0.25 per mile. Ocean Blue Car Rental charges $60 per day and $0.20 per mile. Which company, if either, allows him to travel more miles for the 2 days, and how many miles more?
(Note: Taxes are already included in the rental charges)View SolutionWhen there are x milligrams of a certain drug in a patient's bloodstream, a patient's heart rate, h, in beats per minute, can be modeled by the equation h=60+0.5x. Which statements are true?
I. 10 minutes after taking the drug, the patient's heart rate increase to 75 beats per minute.
II. When the drug is not in the bloodstream, the patient's heart rate is 70 beats per minute.
III. For each 10 milligram increase of the drug in the patient's bloodstream, the patient's heartbeat increase 5 beats per minute.View SolutionBryan, who works in a high-end jewelry store , earns a base pay of $10,00 per hour plus a certain percent commission on the sales that he helps to broker in the store. Bryan worked and average of 35 hours per week over the past two weeks and helped to broker sales of $5,000.00 worth of jewelry during that same two-week period. IF bryan's earnings for the two-week period were $850.00, what percent commission on sales does Bryan earn?
View Solution

