Question

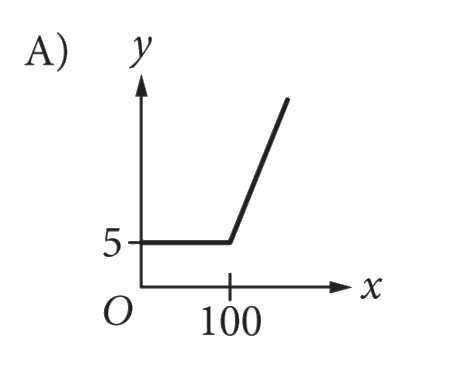
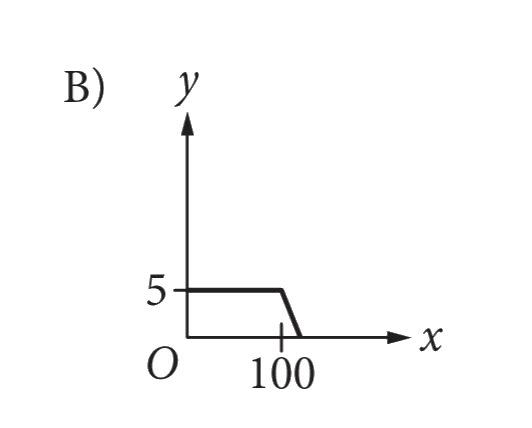
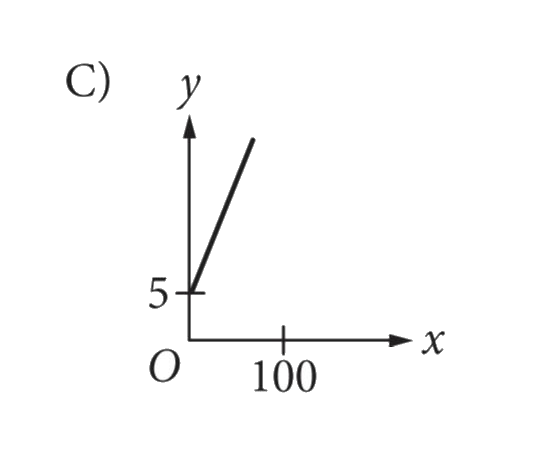
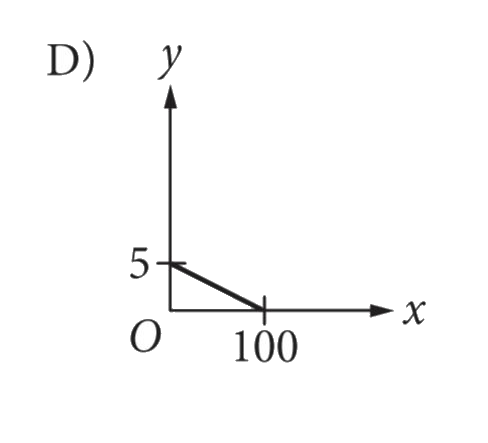
A text messaging plan charges a flat fee of $5 per month for up to 100 text messages sent plus $0.25 for each additional text message sent that month. Which of the following graphs represents the cost, y, of sending x texts in a month?

Options

A.
B.
C.
D.

Answer

A

Explanation

To solve the problem, we need to analyze the text messaging plan and determine how the cost $$y$$ changes with the number of text messages sent $$x$$.

1. Understand the Pricing Structure:
- The plan charges a flat fee of $5 for up to 100 text messages.
- For any text messages sent beyond 100, there is an additional charge of $0.25 for each extra message.

2. Define the Cost Function:
- For \( x \) (the number of text messages) less than or equal to 100:
\( y = 5 \)
- For \( x \) greater than 100:
\( y = 5 + 0.25(x - 100) \)
- This means that for every additional text message sent beyond 100, the cost increases by $0.25.

3. Graph the Cost Function:
- For \( 0 \leq x \leq 100 \), the cost \( y \) is constant at $5. This will be a horizontal line at \( y = 5 \).
- For \( x > 100 \), the cost will increase linearly. The slope of this line is \( 0.25 \), starting from the point \( (100, 5) \).

4. Identify the Characteristics of the Graph:
- The graph should show a horizontal line at \( y = 5 \) for \( x \) from 0 to 100.
- After \( x = 100 \), the graph should show a line that rises with a slope of \( 0.25 \).

5. Evaluate the Given Graph Options:
- We need to find a graph that matches the characteristics described above:
- A horizontal line at \( y = 5 \) for \( x \) from 0 to 100.
- A line that increases after \( x = 100 \).

6. Select the Correct Graph:
- After evaluating the options, we find that:
- Option A shows a horizontal line at \( y = 5 \) for \( x \leq 100 \) and then a line that increases after \( x = 100 \).
- Option B shows a decrease in cost after \( x = 100 \), which is not possible according to the pricing structure.

Conclusion:
The correct graph that represents the cost \( y \) of sending \( x \) texts in a month is Option A.