If O=(0,0), A=(1,0) and B=(1/2,√3/2) then the centre of the circle for which the lines OA, Ab and BO are the tangents, is Solution in Telugu
(12,12√3)
(12,14)
(12,−1√3
(12,√34)
The correct Answer is:A
Step by step video, text & image solution for If O=(0,0), A=(1,0) and B=(1//2, sqrt3//2) then the centre of the circle for which the lines OA, Ab and BO are the tangents, is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Exercise 1C(Pole, Polar)
107 Videos
- CIRCLEBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Exercise 1D(Angle Between Circles)
49 Videos
- CIRCLEBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Exercise 1A(Circle)
110 Videos
- BINOMIAL THEOREMBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET - 4
4 Videos
- COMPLEX NUMBERS BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - COMPLEX NUMBERS EXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) (SET - 4)
5 Videos
Similar Questions
The polar of the point (3,4) w.r.t. x2+y2=25 is
View SolutionThe number of common tangents that can be drawn to the circles x2+y2−4x+6y+8=0,x2+y2−10x−6y+14=0
View SolutionThe equation of the circle with centre (3, -2) and radius 3 is
View SolutionA : If the coefficients of 5th, 6th , 7th terms of (1+x)n are in A.P. then n=7or14.
R : If the coefficients of rth, (r+1)th,(r+2)th terms of (1+x)n are in A.P. then n2−(4r+1)n+4r2=2.
View SolutionA : If argument of z1=π/3 , argument of z2=π/4 then argument of z1z2 is 7π/12
R : Arg (z1z2)=Argz1+Argz2
View Solutionif P=(0,0),Q=(1,0) and R=((1)/(2),(sqrt(3))/(2)), then the centre of the circle for which the lines PO,QR and RP are tangents is
View SolutionIf A(0,0),B(1,0) and C((1)/(2),(sqrt(3))/(2)) then the centre of the circle for which the lines AB,BC,CA are tangents is
View SolutionA circle passes through (0,0) and (1,0) and touches the circle x^(2)+y^(2)=9 then the centre of circle is -
View SolutionTwo circles with centres A and B touch each other internally. Another circle touches the larger circle internally at the point X and the smaller circle externally at the point Y. If O be the centre of that circle, prove that (OA + BO) is constant.
View SolutionThe straight line PAB intersects the circle with centre O at the points A and B. The straight line PAB will be a tangent to that circle if AB=_______
View SolutionIf P(0,0,)Q(1,0)andR(12,√32) are three given points, then the centre of the circle for which the lines PQ,QR and RP are the tangents is
View Solutionयदि मूलबिंदु O से वृत्त x2+y2−6x−8y+21=0 पर खींची गई स्पर्श रेखाएं OA व OB हैं तब AB की लम्बाई है
View SolutionIn the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
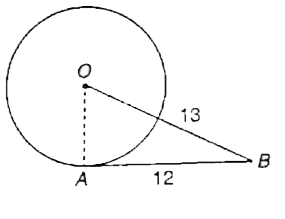
View SolutionA,B are conjugate points w.r.t circle having centre O radius r then OA2+OB2−2r2=AB2
View SolutionIf O=(0,0),A=(1,0) and B=(12,√32) then centre of circle for which the lines OA, OB and AB are tangents is
View Solution
