A block B is pushed momentarily along a horizontal surface with an initial velocity v . If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:

vgμ
gμv
gv
vg
The correct Answer is:A
μ=fN=mamg=ag
⇒ Retardation , a = μ g
Using , v = u + at , 0 = v −μ gt
t=vμg
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - More than one correct
18 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Assertion - Reason
12 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Problem For Practice
23 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston
14 Videos
Similar Questions
A rectangular block is kept on a rough horizontal surface and given some initial velocity. The coefficient of friction between the block and the surface is constant. The block will topple
View SolutionA block begins to move on a rough horizontal surface with an initial velocity u. If it loses of its initial kinetic energy in time t, the coefficient of kinetic friction between the block and the surface is
View Solution
Knowledge Check
A body is moving along a rough horizontal surface with an initial velocity 6m/s m If the body comes to rest after travelling 9 m , then the coefficient of sliding friction will be
A0.4B0.2C0.6D0.8A wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle with the horizontal. If is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -
AFM(cosϕ+μsinϕ)−μgBFsin(ϕ)MCμFcosϕD,uFsinϕA block of mass 2kg is given a push for a moment horizontally and then the block starts sliding over a horizontal plane. The graph shows the velocity− time of the motion. The co− efficient of sliding friction between the plane and the block is :
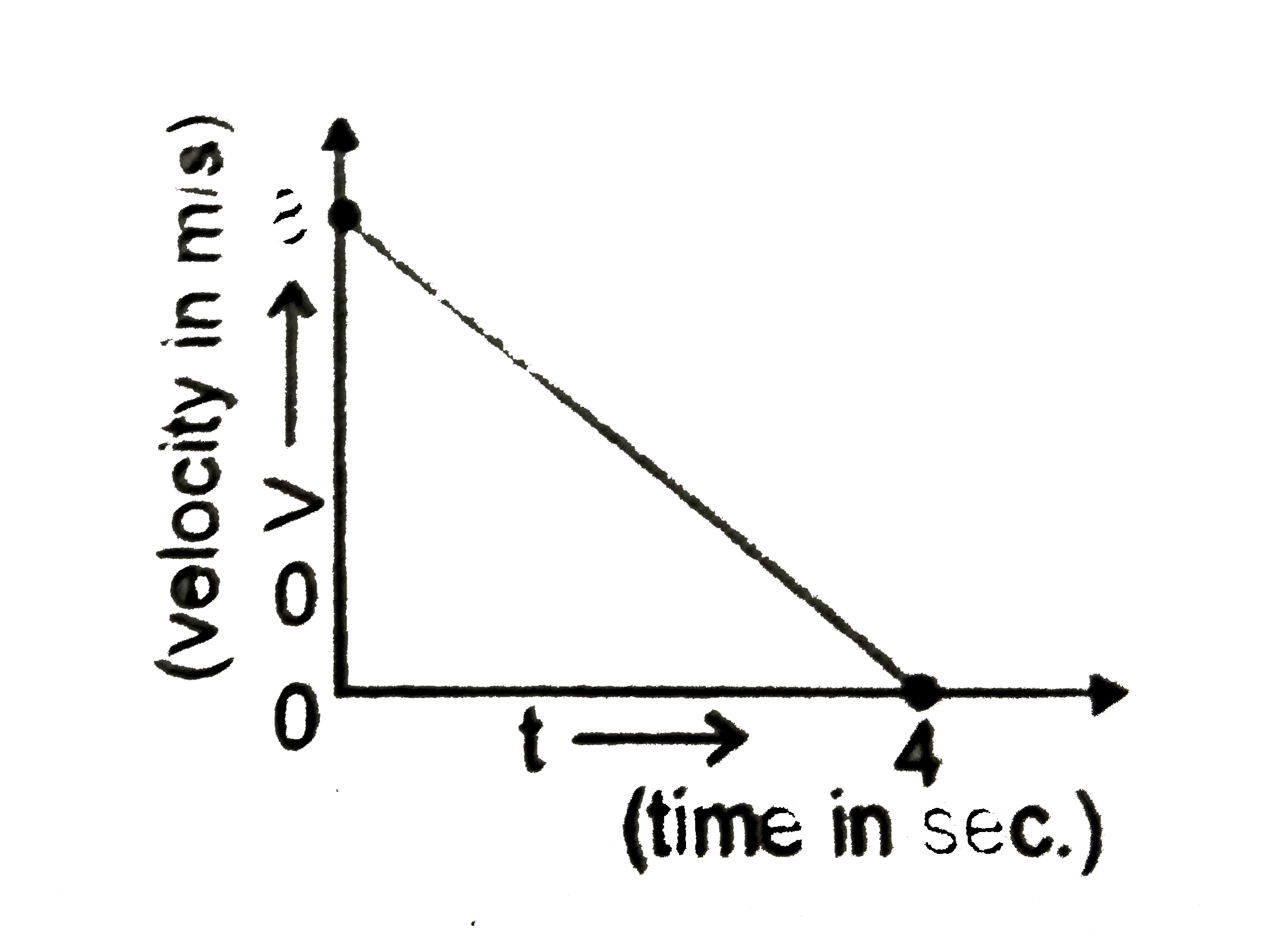 A0.02B0.20C0.04D0.40
A0.02B0.20C0.04D0.40
A block of mass m lying on a rough horizontal surface of friction coefficient μ is pulled by a force F as shown , the limiting friction between the block and surface will be
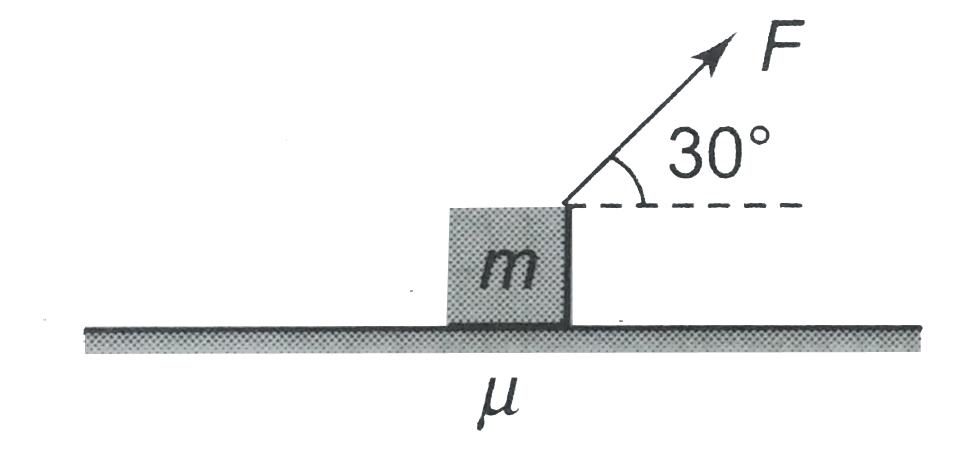
View SolutionA varying horizental force F=at act on a block of mass m kept on a smooth horizontal surface An identical block is kept on the first block.The coefficient of friction between the blocks is μ . The time after which the relative sliding between the blocks prevails is
View SolutionSTATEMENT-1: A block of mass m starts moving on a rough horizontal surface with a velocity v. It stops due to friction between the block and the surface after moving a certain distance. The surface is now tilted to an angle of 30∘ with the horizontal and the same block is made to go up on the surface with the same initial velocity v. The decrease in the mechanical energy in the second situation is smaller than that in the first situation.
because
STATEMENT-2: The coefficient of friction between the block and the surface decreases with the increase in angle of inclination.
View SolutionAsseration : A block of mass m starts moving on a rough horizontal surface with a velocity v. It stops due to friction between the block and the surface after moving through a ceratin distance. The surface is now tilted to an angle of 30∘ with the horizontal and same block is made to go up on the surface with the same initial velocity v. The decrease in the mechanical energy in the second situation is small than the first situation.
Reason : The coefficient of friction between the block and the surface decreases with the increase in the angle of inclination.
View SolutionA block of mass M is using on a rough horizontal surface. μR is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View Solution
