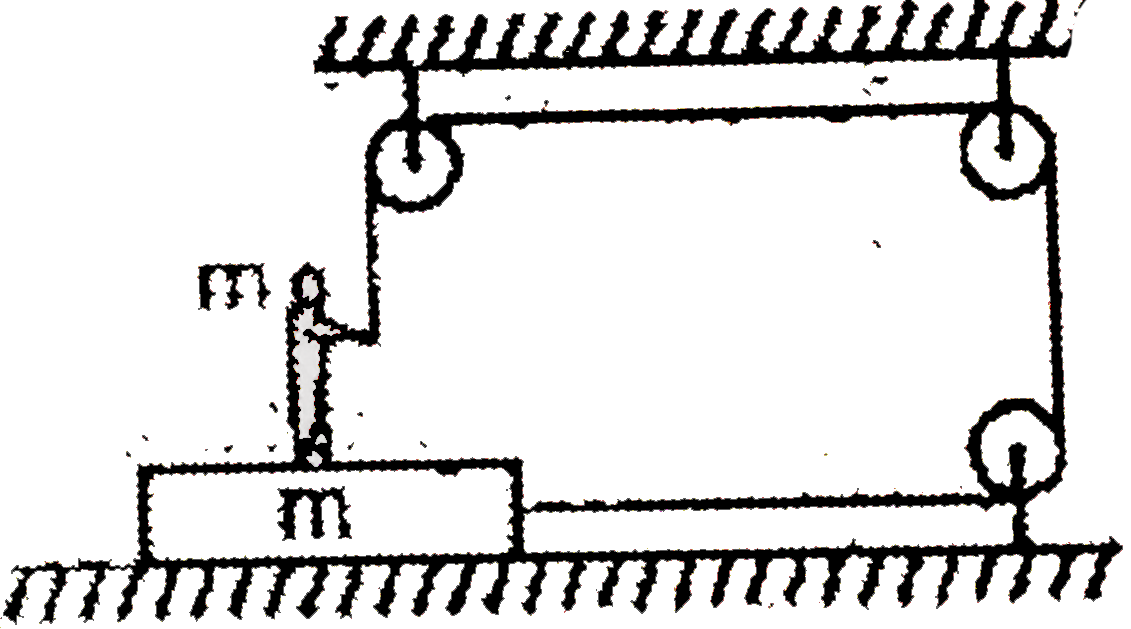
The friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

The force acting on the system are shown in Fig. 7.47

For vertical equilibrium of the point P
 ...... (i)
...... (i)
And for vertical equilibrium of the system∗
R+T(m+M)g , i.e. , R = (m + M) g-T ......(ii)
Now the system will not move horizontally till
T<fL
i.e., T<μ[(m+M)g−T] (fL=μR)
which on simplification gives
T<μ(m+M)g(1+μ)
So , in the light of eqn. (i), we get
Fmax=μ(m+M)g(1+μ)
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Problem For Practice
23 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - OBJECTIVE QUESTIONS ( only one choice is correct )
80 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston
14 Videos
Similar Questions
The friction coeficient bettween the board and the floor shownin filgure is μ. Find the maximum force that the man can exert on the rope so tht the board does not slipon the floor.

View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=03, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View Solution
Knowledge Check
The friction coefficient between the plank and floor is μ. The man applies, the maximum possible force on the string and the system remains at rest. Then :
 Afriction force between plank and surface is 2μmg1+μBfrictional force on man is zeroCtension in the string is 2μmg1+μDnet force on man is zero
Afriction force between plank and surface is 2μmg1+μBfrictional force on man is zeroCtension in the string is 2μmg1+μDnet force on man is zeroA ladder wighing 300 N is placed against a smooth vertical wall having a coefficient of friction between it and the floor of 0.2. What is the maximum force of friction available at the point of contact between the ladder and the floor?
A40 NB50 NC60 ND70 N
If the coefficient of friction between the wedge A and block B shown in the figure is μ, then the maximum possible horizontal acceleration of A for which B doesn’t slip is [ angle of inclination of wedge = 45∘ ]

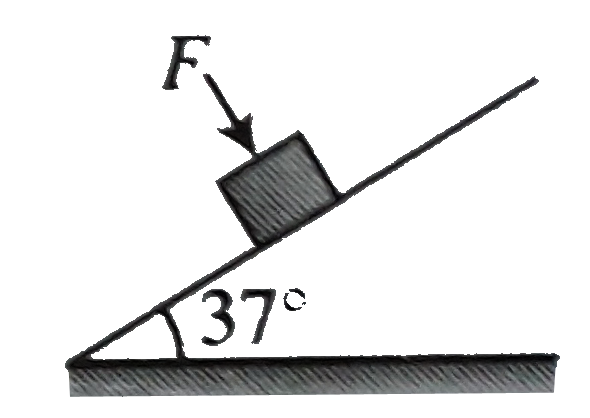
View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ as shown in figure The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?
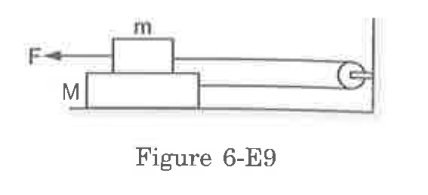
View SolutionThe friction coefficient between the two blocks shown in figure is μ but the floor is smooth. A. What maximum horizontal force F can be applied without disturbing the equilibrium of the systme? b.suppose the horizontal force applied is double of that found in part a. Findthe accelerations of the two masses.
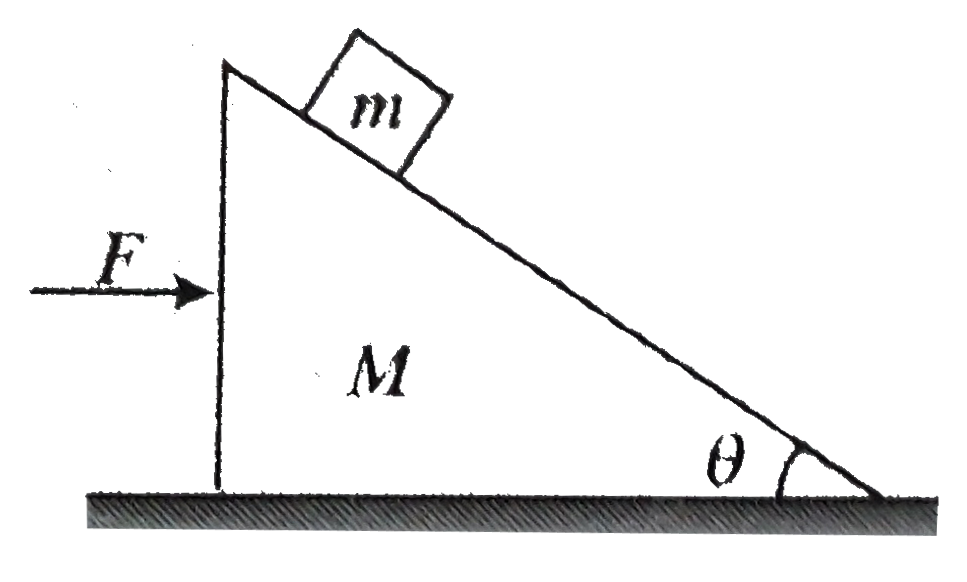
View SolutionA bar of mass m is placed on a triangular block of mass M as shown in figure The friction coefficient between the two surface is μ and ground is smooth find the minimum and maximum horizontal force F required to be applied on block so that the bar will not slip on the inclined surface of block
View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionA uniform board of length L is sliding along a smooth (frictionless) horizontal plane as in figure. The board then slides across the boundary with a rough horizontal surface. The coefficient of kinetic friction between the board and the second surface surface is μk

a. Find the acceleration of the board at the moment its front end has traveled a distance x beyond the boundary.
b. The board stops at the moment its back end reaches the boundary, as in figure. Find the initail speed v of the board.
View Solution
