In a two dimensional motion of a particle, the particle moves from point A, with position vector →r1 to point B, with position vector →r2. If the magnitudes of these vectors are, respectively, r1=3 and r2=4 and the angles they make with the x-axis are θ1=75∘ and θ2=15∘, respectively, then find the magnitude of the displacement vector.

√3
√13
√5
√1
The correct Answer is:B
Step by step video, text & image solution for In a two dimensional motion of a particle, the particle moves from point A, with position vector vec(r )_(1) to point B, with position vector vec(r )_(2). If the magnitudes of these vectors are, respectively, r_(1 )=3 and r_(2)=4 and the angles they make with the x-axis are theta_(1)=75^(@) and theta_(2)=15^(@), respectively, then find the magnitude of the displacement vector. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTOR BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 2
33 Videos
- VECTOR BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 3
18 Videos
- VECTOR BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 3
18 Videos
- UNITS AND DIMENSIONS, BASIC MATHEMATICS BOOK - MOTIONCHAPTER - UNITS AND DIMENSIONS, BASIC MATHEMATICS EXERCISE - PRACTICE QUESTION
4 Videos
- VECTOR & CALCULUSBOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - EXERCISE -4 (LEVEL - II) PREVIOUS YEAR
15 Videos
Similar Questions
Position vector of centre of two particles of masses m1 and m2 whose position vectors r1 and r2 then rcm?
View SolutionA particle moves from position A to position B in a path as shown in If the poit vectors →r1 and →r2 making an angle θ between them are give, find the magnitude of displacement.
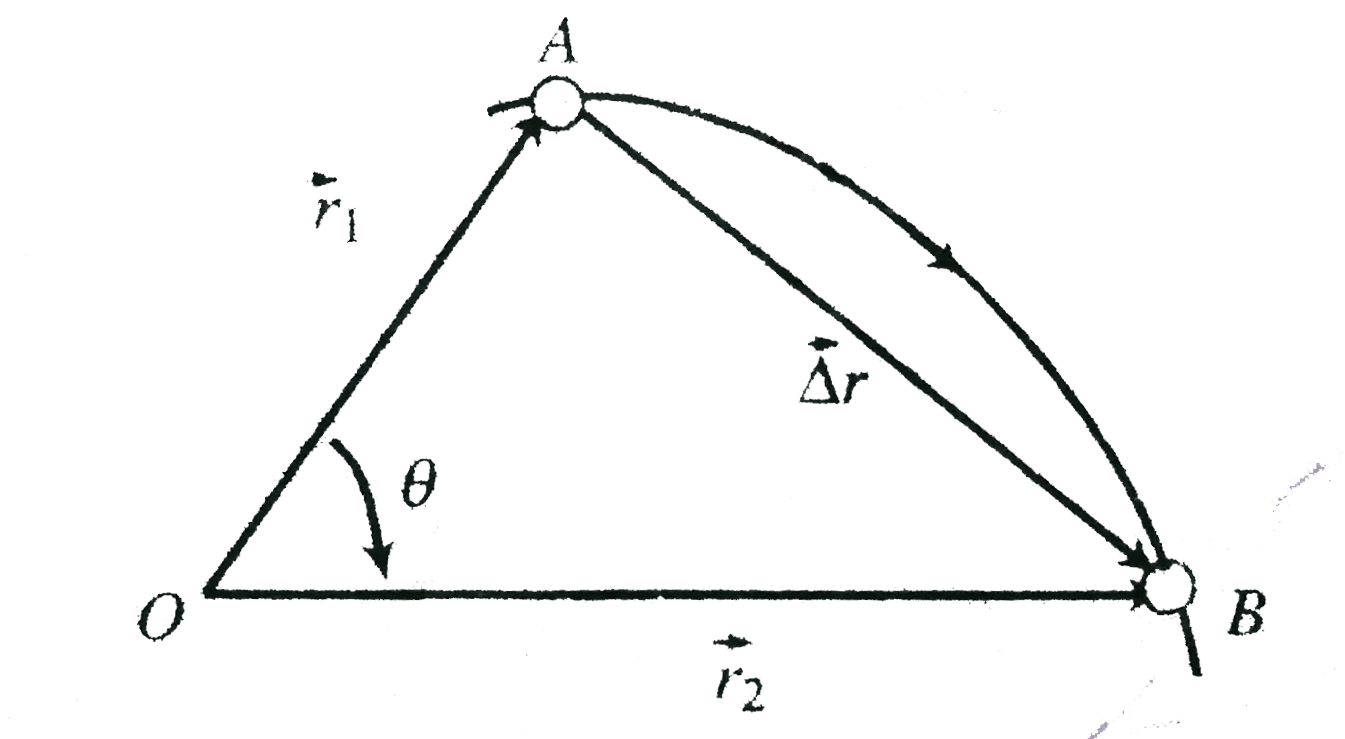 .
.
View Solution
Knowledge Check
In a two diamensional motion of a particle, the particle moves from point A, with position vector →r1 to point B, with position vector →r2. If the magnitudes of these vectors are, respectively, r1=3 and r2=4 and the angles they make with the x-axis are θ1=75∘ and θ2=15∘, respectively, then find the magnitude of the displacement vector.
 A15B√13C17D√15
A15B√13C17D√15In a two-dimensional motion of a particle, the particle moves from point A of position vector →r1, to point B of vectors are , respectively, r1=3andr2=4 and the angles they make with the x axis are θ1=75∘andθ2=15∘, respectively, then find the magnitude of the displacement vector.
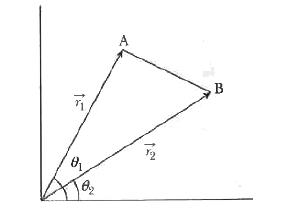 A15B√13C17D√15
A15B√13C17D√15The displacement of a particle from a point having position vector 2ˆi+4ˆj to another point having position vector 5ˆj+1ˆj is
A3 unitsB3√2 unitsC5 unitsD5√3units
Find the position vector of the point, which divides the join of points with position vectors 3→a−2→b and 2→a+3→b in the ratio 2 : 1.
View SolutionFind the position vector of a point R which divides the line joining the two points P and Q with position vectors −−→OP=2→a+→b and −−→OQ=→a−2→b, respectively in the ratio 1:2 internally and externally.
View SolutionA vector →r is inclined at equal angle to the three axes. If the magnitude of →r is 2√3, find →r.
View SolutionFind the position vector of a point which divides the join of points with position vectors →a−2→b and 2→a+→b externally in the ration 2:1.
View SolutionA vector a makes 30∘ and b makes 120∘ angle with the x-axis. The magnitude of these vectors are 3 unit and 4 unit, respectively. The magnitude of resultant vector is
View Solution
