Add vectors →A,→B and →C which have equal magnitude s of 50 unit and are inclined at angles of 45∘,135∘ and 315∘ respectively from x-axos.
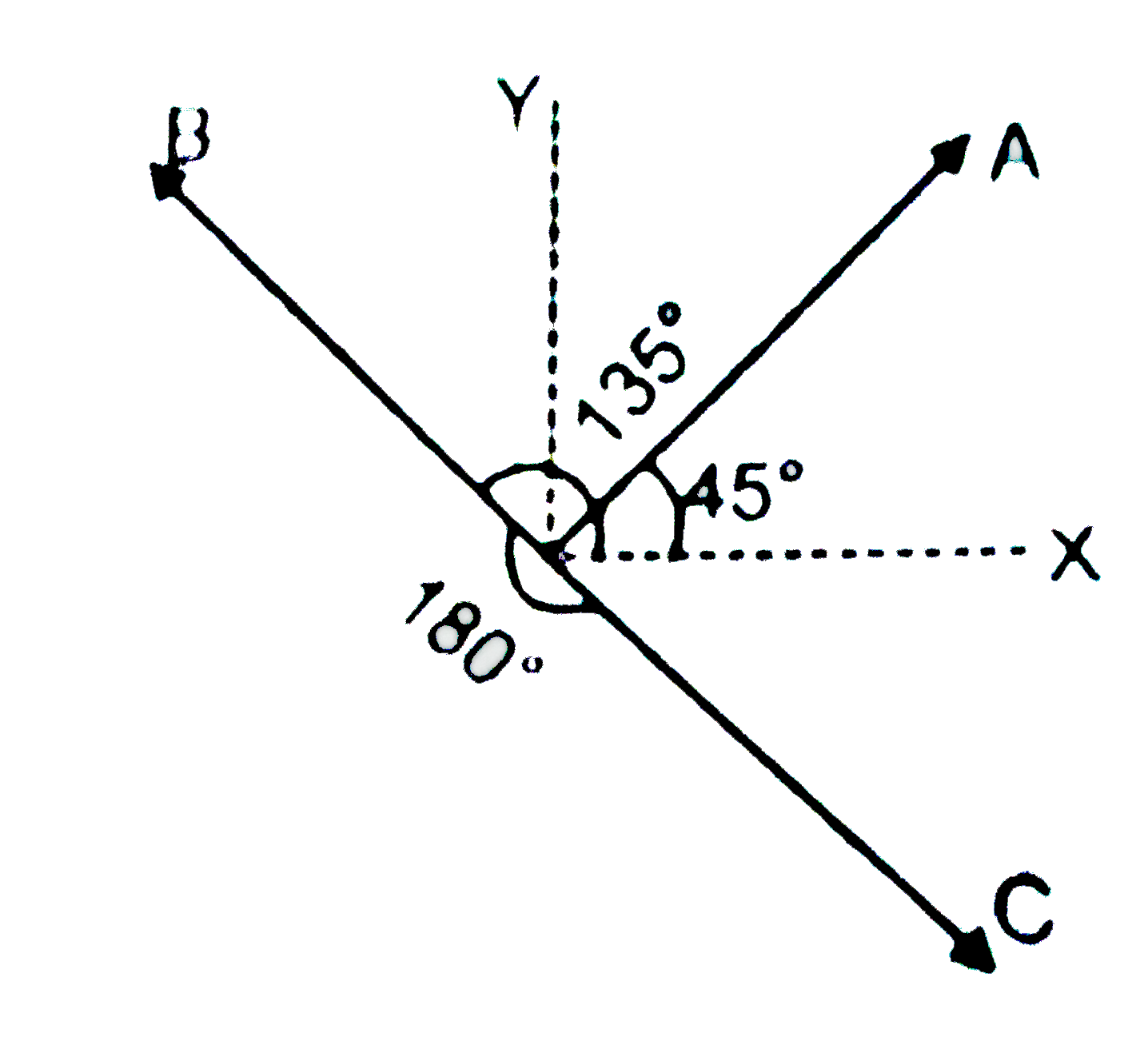
Angle between →Band→C=315∘−135∘=180∘
∴ They balance each other
∴ sum =→A=50 unit at 45∘ from X-axis
Topper's Solved these Questions
- VECTOR BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 1
36 Videos
- VECTOR BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 2
33 Videos
- UNITS AND DIMENSIONS, BASIC MATHEMATICS BOOK - MOTIONCHAPTER - UNITS AND DIMENSIONS, BASIC MATHEMATICS EXERCISE - PRACTICE QUESTION
4 Videos
- VECTOR & CALCULUSBOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - EXERCISE -4 (LEVEL - II) PREVIOUS YEAR
15 Videos
Similar Questions
Knowledge Check
The vector sum of three vectors→A,→B and →C is zero . If ˆi and ˆj are the unit vectores in the vectors in the directions of →A and →B respectively , them :
A→C is in the plane of ˆi of ˆjB→C is along ˆi׈jC→C is along ˆiD→C is alongˆjIf →aand→b are unit vectors inclined to x-axis at angle 30∘and120∘ then ∣∣→a+→b∣∣ equals
A√2/3B√2C√3D2Theree coplanar vectors →A,→B and →C have magnitudes 4.3 and 2 respectively. If the angle between any two vectors is 120∘ then which of the following vector may be equal to 3→A4+→B3+→C2
 A
A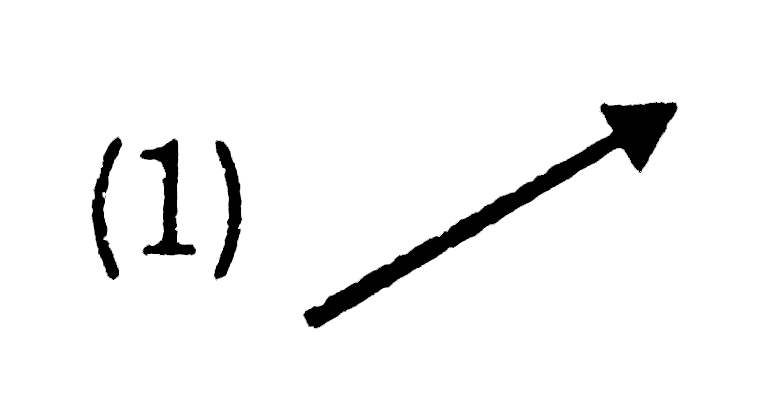 B
B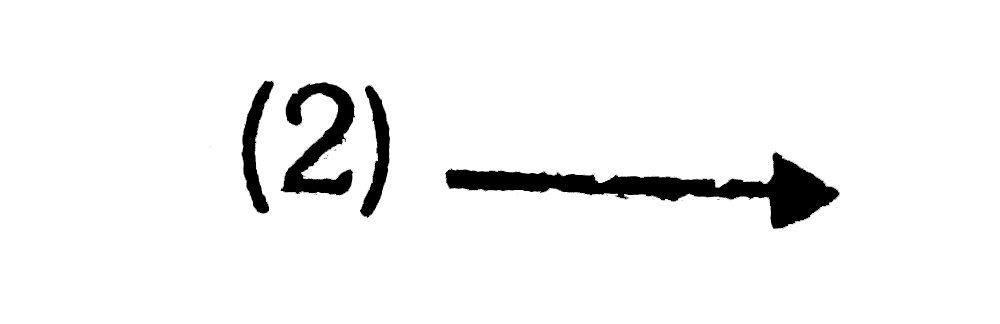 C
C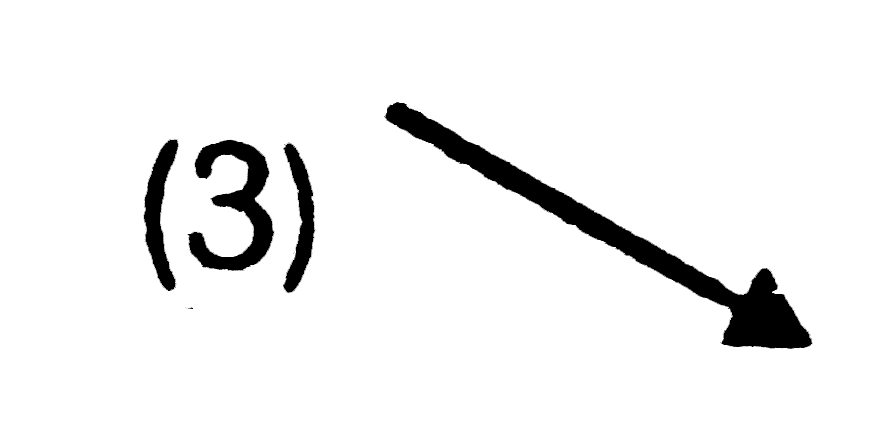 D
D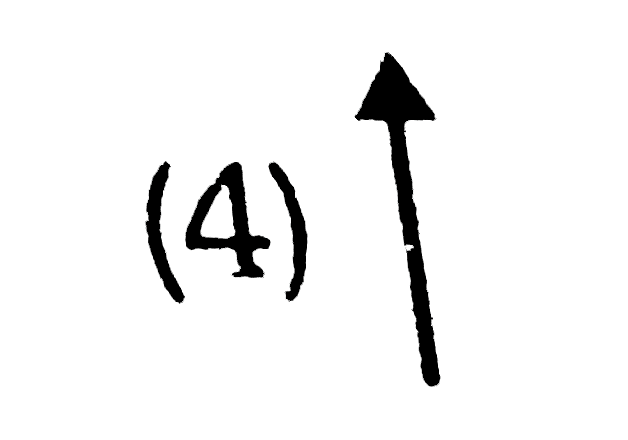
There vectors →a,→b and →c each have a magnitude of 50 m and lie in an xy plane. Their directions relative to the positive direction of the x axis are 30∘,195∘,and315∘, respectively. What are (a) the magnitude and (b) the angle of the vector →a+→b+→c, and (c ) the magnitude and (d) the angle of →a−→b−→c ? What are the (e) magnitude and (f) angle of a fourth vector →d such that (→a+→b)−(→c+→d)=0 ?
View SolutionThree vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →C
View Solutionif →a,→band→c are mutally perpendicular vectors of equal magnitudes, then find the angle between vectors and →a+→b+→c.
View SolutionA magnitude of vector →A,→B and →C are respectively 12,5 and 13 units and →A+→B=→C then the angle between →A and →B is
View SolutionIf →A=→B+→C and the magnitudes of →A,→Band→C are 5,4 and 3 units respecetively, the angle between →A and →C is :
View Solution
