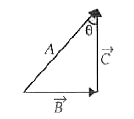
If →A=→B+→C and the magnitudes of →A,→Band→C are 5,4 and 3 units respecetively, the angle between →A and →C is :
cos−1(35)
cos−1(45)
π2
sin−1(34)
The correct Answer is:A
Given : A=∣∣→A∣∣=5,B=∣∣→B∣∣=4
C=∣∣→C∣∣=3
As 52=42+32
A2=B2+C2
∴ Angle between →B and →C is 90∘.
If θ is the angle between →A and →C then
cosθ=CA=35
θ=cos−1(35)
Topper's Solved these Questions
- KINEMATICS Book:MTG-WBJEEChapter:KINEMATICS Exercise:WB JEE WORKOUT ( CATEGORY 3 : One or More than One Option Correct Type (2 Marks))
Explore 10 Videos
- KINEMATICS Book:MTG-WBJEEChapter:KINEMATICS Exercise:WB JEE Previous Years Questions (CATEGORY 1 : Single Option Correct Type (1 Mark) )
Explore 9 Videos
- KINEMATICS Book:MTG-WBJEEChapter:KINEMATICS Exercise:WB JEE Previous Years Questions (CATEGORY 3 : One or More than One Option Correct Type (2 Marks) )
Explore 1 Video
- HEAT AND THERMAL PHYSICSBook:MTG-WBJEEChapter:HEAT AND THERMAL PHYSICSExercise:WB JEE PREVIOUS YEARS QUESTIONS
Explore 15 Videos
- KINETIC THEORY OF GASES Book:MTG-WBJEEChapter:KINETIC THEORY OF GASES Exercise:WB JEE PREVIOUS YEARS QUESTIONS (MCQ)
Explore 7 Videos
Similar Questions
Three vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →C
View SolutionLet →a,→band→c be three unit vectors such that →a is perpendicular to the plane of →b and →c. if the angle between →band→c is π3, then ∣∣→a×→b−→a×→c∣∣2 is equal to
View Solution
Knowledge Check
The magnitudes of vectors →A,→Band→C are 3,4 and 5 units respectively. If →A+→B=→C, the angle between →A and →B is
Aπ2Bcos−1(0.6)Ctan−1(75)Dπ4Given : →C=→A+→B . Also , the magnitude of →A,→Band→C are 12,5 and 13 units respectively . The angle between →Aand→B is
A0∘Bπ4Cπ2DπA magnitude of vector →A,→B and →C are respectively 12,5 and 13 units and →A+→B=→C then the angle between →A and →B is
A0BπCπ/2Dπ/4
If →a,→b,→c are unit vectors such that veca is perpendicular to →band→cand∣∣→a+→b+→c∣∣=1 then the angle between →band→c is (A) π2(B)pi(C)0(D)(2pi)/3
View SolutionThe magnitudes of vectors →A.→B and →C are respectively 12,5 and 13 unira and →A+→B=→C, then the angle between →A and →B is :
View SolutionIf →A=→B+→C and the magnitudes of →A,→Band→C are 5,4 and 3 units respecetively, the angle between →A and →C is :
View SolutionIf →a+→b+→c=→0,|→a|=3,∣∣→b∣∣=5and|→c|=7 , then the angle between →aand→b is
View Solution→A,→Band→C are vectors such that →C=→A+→Band→C⊥→A and also C= A . Angle between →Aand→B is :
View Solution

