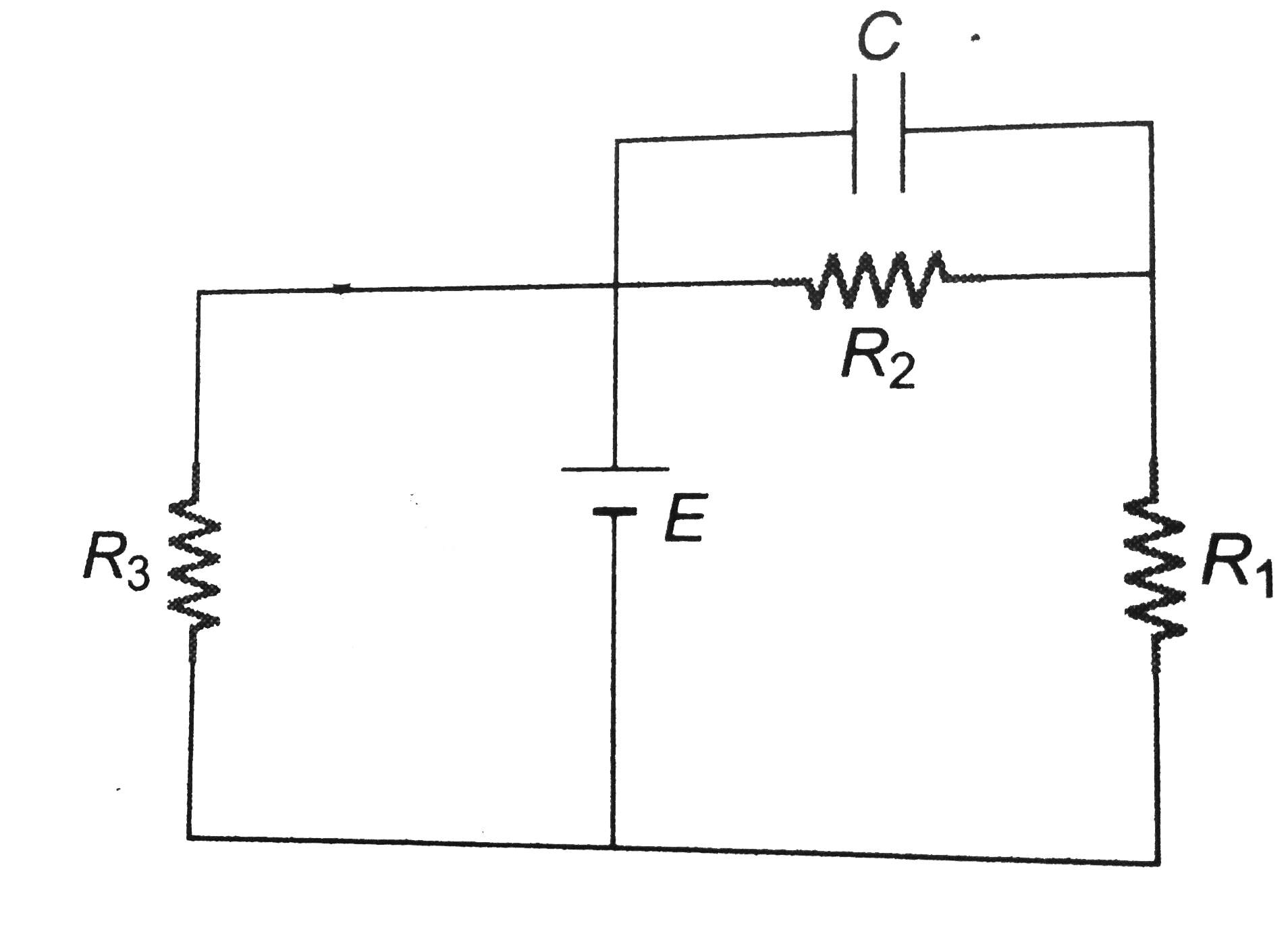
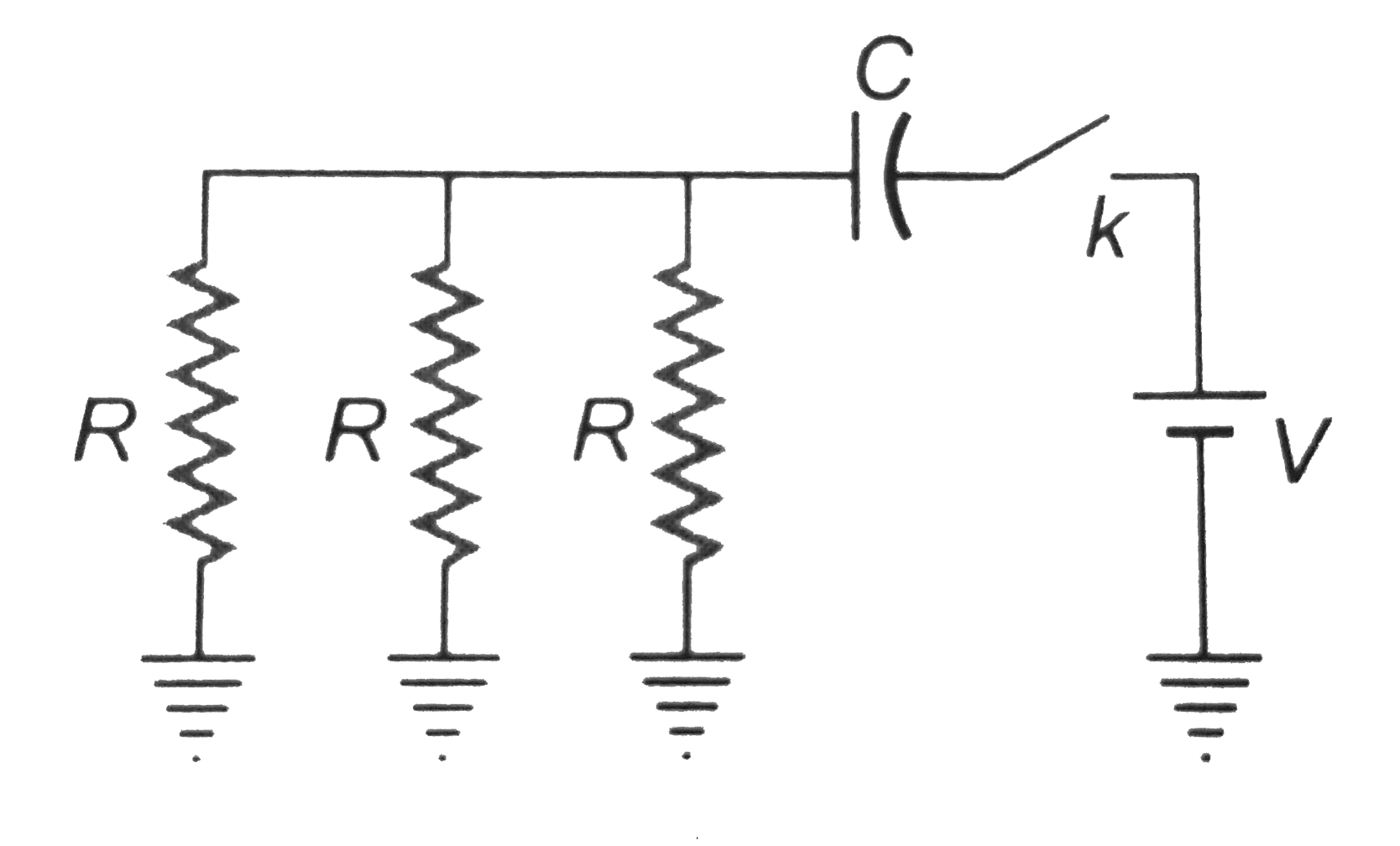
Initially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

Applying KVL in loop ABCDA
∈−iR−(i−i1)R=0
∈−2iR+i1R=0
Applying KVL in loop ABCEFDA
∈−iR−i1R−qc=0
(##MOTCONJ∃PHYC25SLV041_S01.png width=80%><br> (2in -in - i_1R -2i_1R) /( 2) =(q)/(c ) <br> in C - 3i_1 RC = 2q<br> in C - 2q =3( dq)/( dt) RC.<br>int _0^(q) (dq)/( in C - 2q) = int _0 ^(t) rArr -(1)/(2) 1n (in C -2q)/( in C) =(t)/( 3RC) <br> q =(in C)/(2) ( 1-e^(-2t//RC)) <br>Methodforobjective<br>Ina∘uitwhenthereisonlyo≠∩aci→rthen<br> q= Q_(st) (1-e^(-t//rau) ) : Q_(st) = steadystatechan≥on∩aci→r<br> tau =R_(eff) C <br> R_("effective") is the resistance between the capacitor when battery is replaced by its internal resistance
Topper's Solved these Questions
- Capacitance Book:MOTIONChapter:Capacitance Exercise:EXERCISE -1
Explore 60 Videos
- Capacitance Book:MOTIONChapter:Capacitance Exercise:EXERCISE -2
Explore 36 Videos
- CALORIMETRY Book:MOTIONChapter:CALORIMETRY Exercise:EXERCISE - 3 Section - B
Explore 4 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 4 Level-II
Explore 20 Videos
Similar Questions
The charge on the capacitor is initially zero. Find the charge on the capacitor as a function of time t. All resistors are of equal value R.
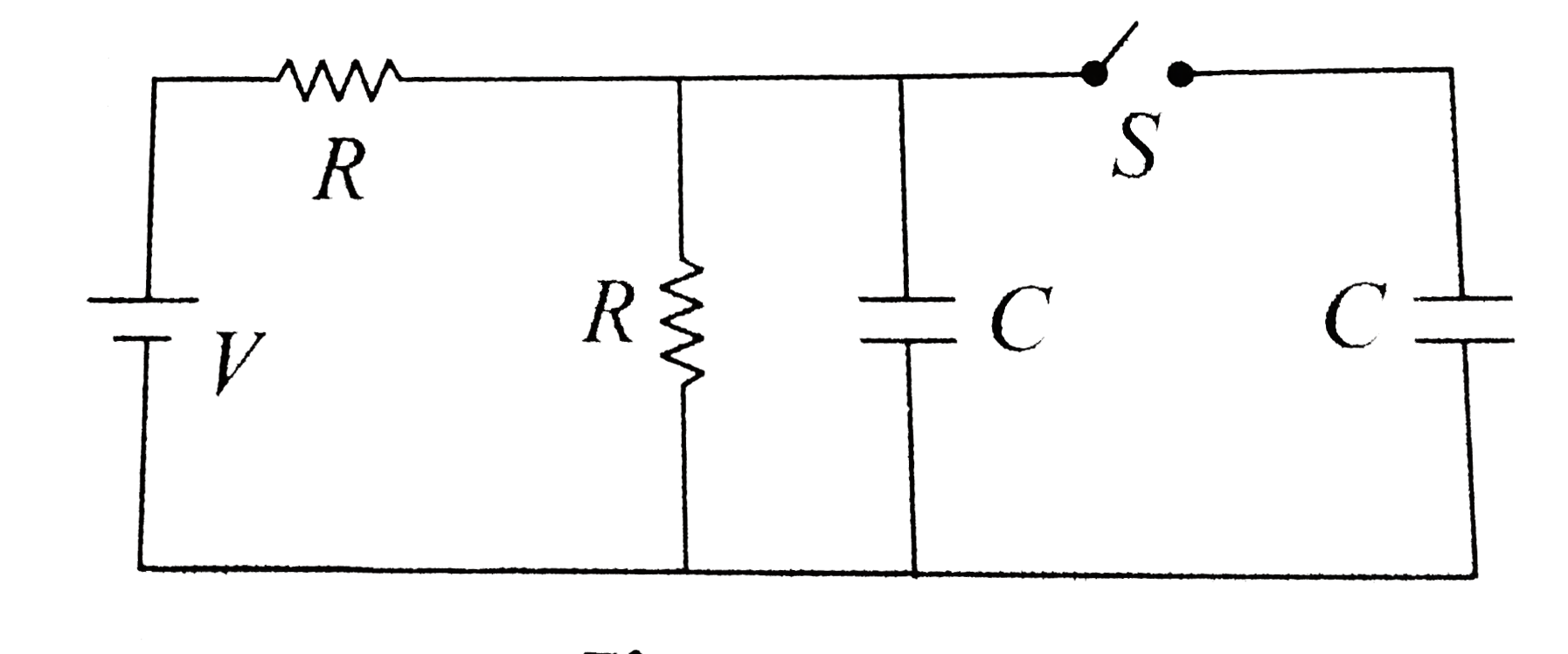
View Solutioninitially the switch is open for a long time. Now the swithc is closed at t=0. find the caharge on the rightomost capacitor as a function of time given that it was initially unchanged.
View Solution
Knowledge Check
Initially the capacitor was uncharged Current in the capacitor just after switching on will be ?
 AεRBε2RCε5RDε4R
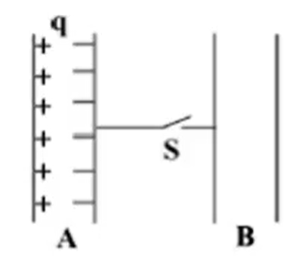
AεRBε2RCε5RDε4RConsider the situation shown in the figure. The capacitor A has a charge q on it whereas B is uncharged. The charge appearing on the capacitor B a long 7 time after the switch is closed is :
 .AzeroBq/2CqDq
.AzeroBq/2CqDqInitially capacitor is uncharged at t=0 switch is closed. Charge on capacitor when current in the circuit is 10% of maximum current :
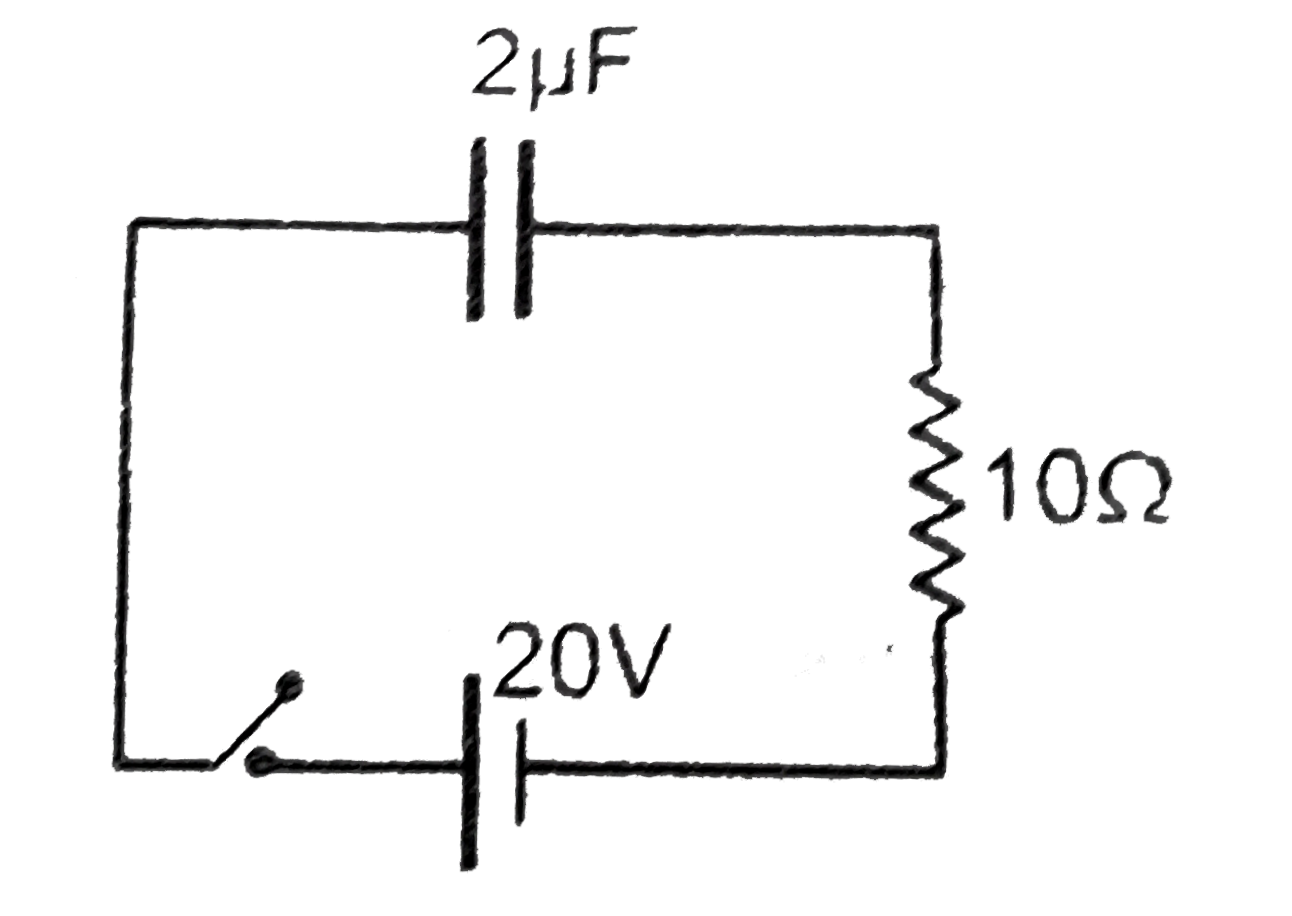 A4μCB8μCC36μCD16μC
A4μCB8μCC36μCD16μC
In figure-5.143 ifS is closed at t=0, find charge on capacitor as a function of time. Time inductor is active with initial current I0 in it.

View SolutionInitially the 900μF capacitor is charged to 100V and the 100μFcapacitor is uncharged in Fig. Then switch S2 is closed for time t1, after which it is opened and at the same instant switch S1 is closed for time t2 and then opened. It is now found that 100μF capacitor is charged to 300μF capacitor is charged to 300V. Find the minimum possible value of the time interval t1 and t2.

View Solution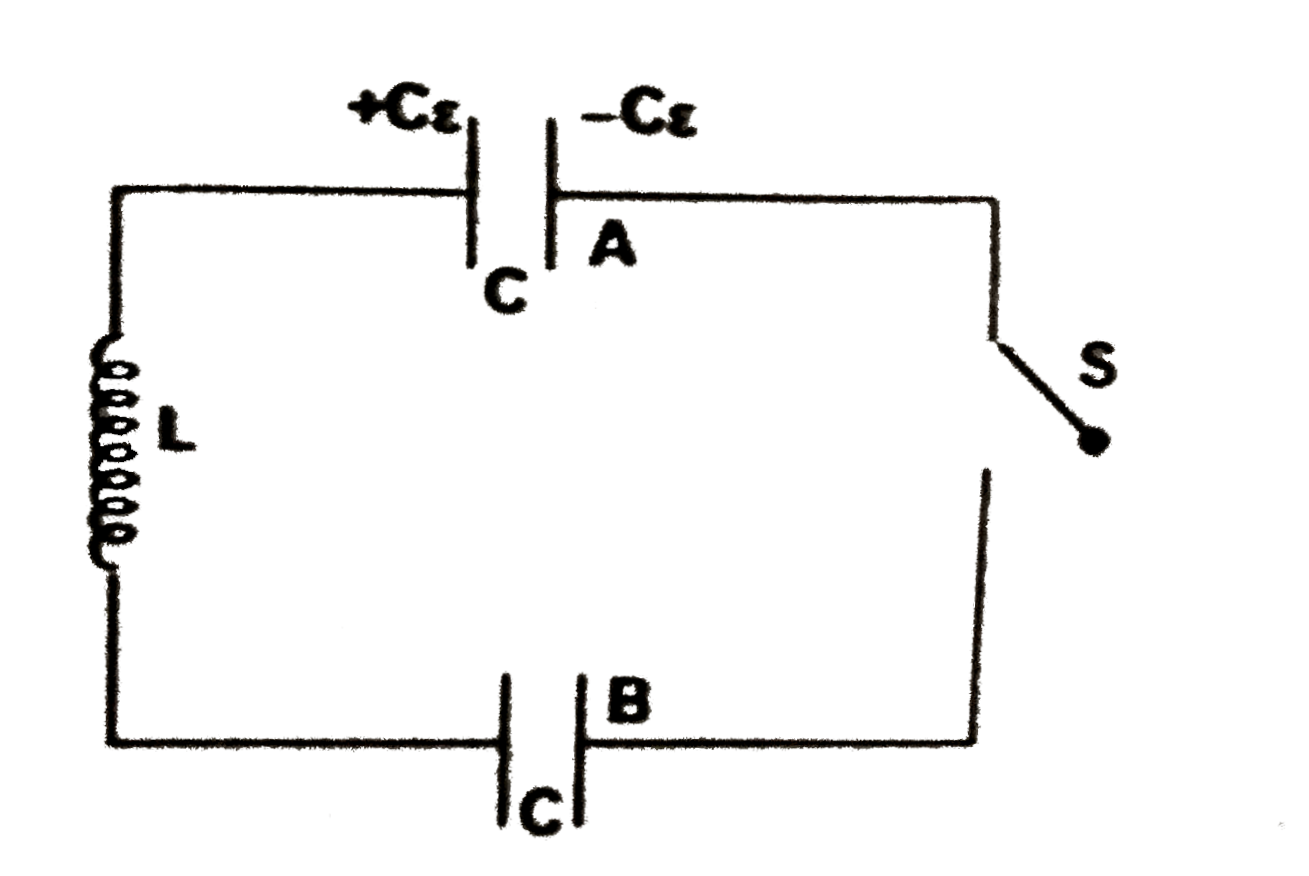
Initially capacitor 'A' is charged to a potential drop ε and capacitor B is uncharged At t=0, switch S is closed, then the maximum current through the inductor is
View SolutionThe switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by
View SolutionConisder the istuation shown in the figure. The capacitor A has a charge q on it whereas B is unchanged. The charge appearing on the capacitor B a long time after the switch is closed is
View Solution