A point light source of 100W is placed at a distance x from the centre ofa hole ofradius R in a sheet as shown in figure, Find the power passing through the hole in sheet

From figure, the solid angle of cone shown in figure can be given as
σ=2π(1−cosθ)=2π(1−x√R2+x2)
Power in hole = power given in solid angle σ
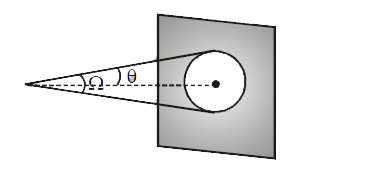
P=1004π×σ
=1004π×2π(1−x√R2+x2)
=50(1−x√R2+x2)watt
Topper's Solved these Questions
- ELECTROSTATICS-IIBOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise 1 (Section A-Questions Based on electric flux for various configuration, Question on solid angle concept, Gauss law Based Questions)
16 Videos
- ELECTROSTATICS-IIBOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise 1 (Section B - Properties of conductors)
15 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
13 Videos
- ERRORS , THEORY BOOK - MOTIONCHAPTER - ERRORS , THEORY EXERCISE - EXERCISE 4 (LEVEL -II)
10 Videos
Similar Questions
A hemisphere of radius R, made of glass of refractive index (3/2) is placed on 'the table. A point source of light is placed at a distance 2R from the centre, of hemisphere. If source is viewed diametrically opposite side of hemisphere. Find the position of image of source.

View SolutionA mono chromatic light source of wave length I is placed at a distance R from the mirror as shown and a spherical screen of radius R is at a distance R from the source as shown in the figure and point P is on the sphere nearest to the source.It R is two times the wave length (R=2l) then f'+(p)
View Solution
Knowledge Check
If two coherent source are placed at a distance 3λ from each other, symmetric to the centre of the circel as shown in figure, Find thenumber of fringes shown on the screen, placed along the circumference ?
 A16B12C8D4
A16B12C8D4A point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R/2 from the centre of the sphere is
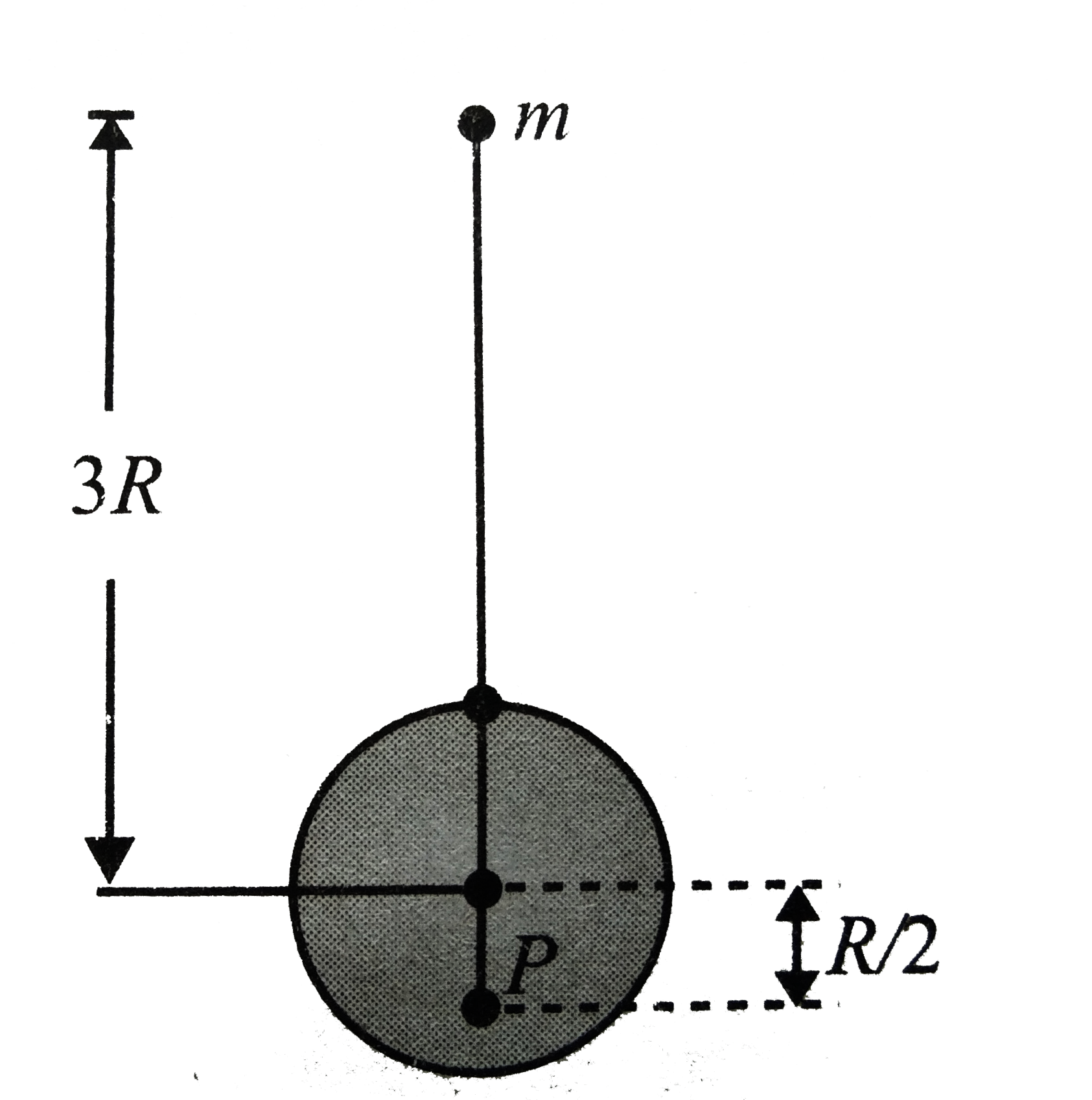 A√2GM3RB√5GM3RC√25GM24RDnone of these
A√2GM3RB√5GM3RC√25GM24RDnone of theseA uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by
 Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)
Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)
Two slits are made on an opaque surface at a separation of 1 mm from each other. A screen is placed at a distance 1 m from the plane of the slits. A small hole is made on the screen at a distance 1 mm from the centre of the screen as shown in the figure. If we observe the light coming out from hole on the other side, then which wavelengths in the visible region will be absent and which will show strong presence ? Wavelength of visible light ranges from 400 nm to 700 nm.

View SolutionA point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.

View SolutionThe figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is

View SolutionFind the position of centre of mass of the uniform planner sheet shown in figure with respect to the origin (O) -
View SolutionIn the figure shown, O is a point source of light and S is a screen placed at a distance L from the source. Intensity of light at point A on the screen due to the source is 81 I where I is some unit. Now a large mirror (M) is placed behind the source at a distance L from it. The mirror reflects 100% of the light energy incident on it. Calculate the inten- sity at point A.
View Solution
