A particle of mass 9×10−31 kg having a negative charge of 1.6×10−19C is projected horizontally with a velocity of 106ms−1 into a region between two infinite horizontal parallel plates of metal. The distance between the plates is d=0.3cm and the particle enters 0.1cm below the top plate, THe top and bottom plates are connected, respectively to the positive and negative terminal of a 30V battery. Find the components of the velocity of the particle just before it hits one of the plates.
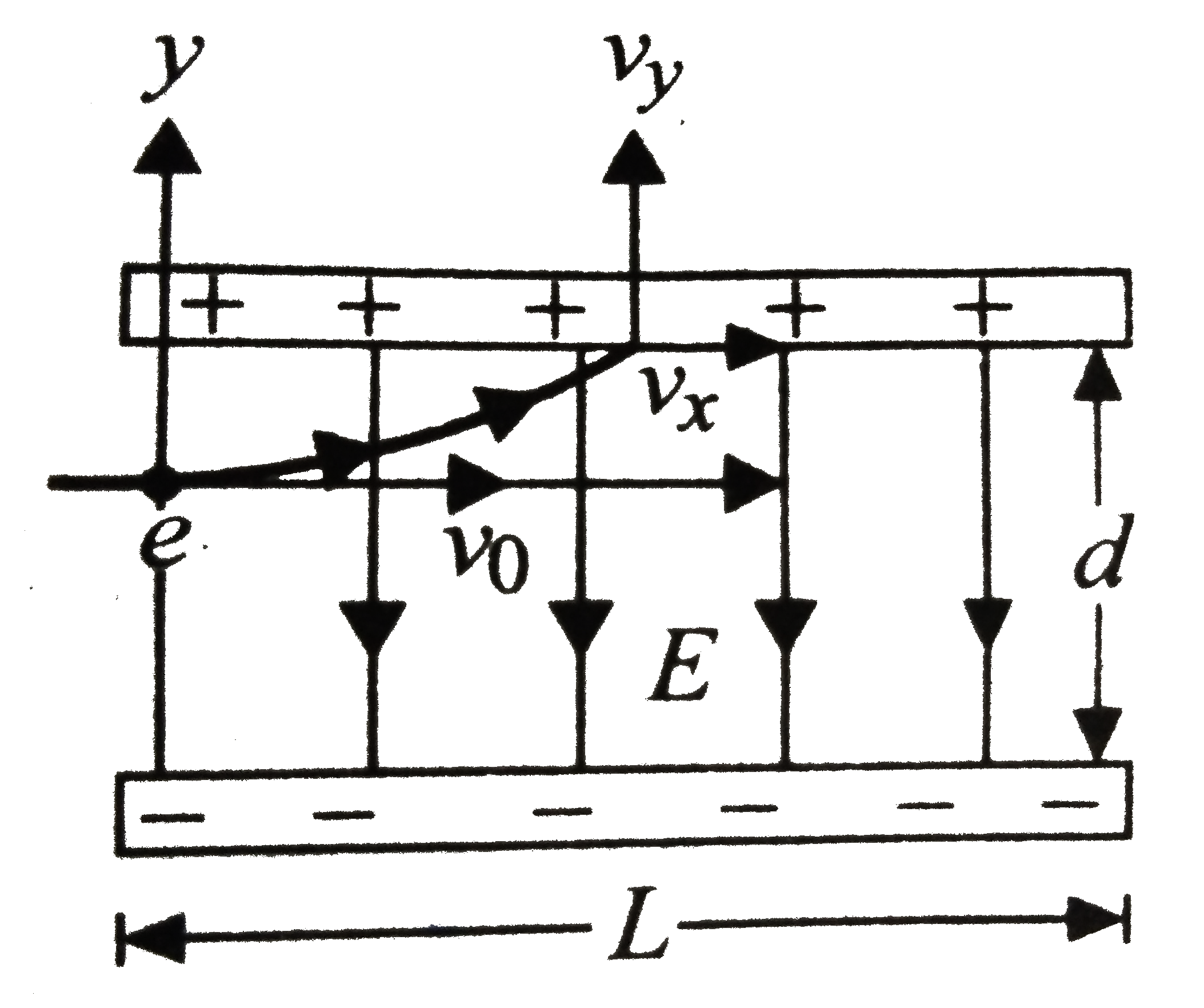
We known that between two parallel plates electric field can be given as
E=Vd
Here V = 30 volt and d = 0.3 cm =3×10−3m
Thus we have E=303×10−3=104N/C
Force on the particle of negative charge moving between the plates
F=e×E=1.6×1019×104=1.6×1015 newton The direction of force will be towards the positive plate i.e., upward.
Now acceleration of the particle is
or a=eEm
or a=(1.6×10−15)/(9×10−31)
or a=1.77×1015m/sec2
As the electric intensity E is acting in the vertical direction the horizontal velocity v of the particle remains same. if y is the displacement of the particle, in upward direction, we have
y=12at2
Here, y=0.1cm=10−3m,a=1.77×1015m/sec2
Thus, 10−3=12×(1.77×10−15)(t2)
Solving we get =1.063×10−10 second component of velocity in the direction of field is given by
Vy=at
=(1.77×1015)(1.063×10−10)
=1..881×104m/s .
Topper's Solved these Questions
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section A)
10 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section B)
10 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (B) Previous Year Problems | JEE Main
30 Videos
- ELECTROSTATICS-IIBOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise - 4 (Level - II)
30 Videos
Similar Questions
A particle of mass 9×10−31 kg having a negative charge of 1.6×10−19C is projected horizontally with a velocity of 106ms−1 into a region between two infinite horizontal parallel plates of metal. The distance between the plates is d=0.3cm and the particle enters 0.1cm below the top plate, THe top and bottom plates are connected, respectively to the positive and negative terminal of a 30V battery. Find the components of hte velocity of hte paricle just before it hits one of the plates.

View SolutionThe capacity of a parallel plate capacitor is 10 μF when the distance between its plates is 9 cm. What will be its capacity if the distance between the plates is reduced by 6 cm.
View Solution
Knowledge Check
In a parallel capacitor the potential difference between the plates is V ,A particle of mass m and charge −Q leaves the negative plate and reaches the positive plate at distance d in time t with a momentum p .Then
Ap=√mQVBp=√2mQVCt=√md2QVDt=√2md2QVThe capacity of a parallel plate capacitor is 10μF, when the distance between its plates is 8 cm. If the distance between the plates is reduced to 4 cm, the new capacity of the parallel plate capacitor will be
A5μFB10μFC20μFD40μFThe capcity of a parallel plate condenser is 10μF, when the distance between its plates is 8cm. If the distance between the plates is reduced to 4cm, then the capacity of this parallel plate condenser will be
A5μFB10μFC20μFD40μF
The plates of a parallel plate capacitance 1.0 F are separated by a distance d =1 cm. Find the plate area .
View SolutionAn electron is projected with an initial velocity of 107ms−1 into an electric field between two parallel plates 1 cm apart. The electron enters the field at a point midway between the plates. If the electron just misses the positivity charged plate as it emerges from the field, find the magnnitude of the electric density between the plates. (Length of each plate is 2 cm, mass of electron=9×10−31kg and charge of electron =1.6×10−19C)
View SolutionA small particale carying a negative charge of 1.6×10−19C ia suspended in equilibrium between the horizontal metal plates 5 cm apart, having a potential difference of 3000 V across them. Find the mass of the particle.
View SolutionA parallel-plate capacitor haas plates of unequal area . The large r plates is connected to the positive terminal of the brttery and the smaller plate to its nagative terminal. Let Q,and Qbe the charges appearing on the positive and negative appearing on the
View SolutionA charged oil drop of mass 9.75×10−15kg and charge 30×10−16C is suspended in a uniform electric field existing between two parallel plates. The field between the plates is (take g=10ms−2)
View Solution
