A small particale carying a negative charge of 1.6×10−19C ia suspended in equilibrium between the horizontal metal plates 5 cm apart, having a potential difference of 3000 V across them. Find the mass of the particle.
To find the mass of the particle suspended between the horizontal metal plates, we can follow these steps:
Step 1: Understand the Forces Acting on the Particle
The particle has a weight (mg) acting downwards and an electric force (Qe) acting upwards due to the electric field between the plates. Since the particle is in equilibrium, these two forces must balance each other.
Step 2: Write the Equation for Equilibrium
Since the particle is in equilibrium:
mg=Qe
Where:
- m = mass of the particle
- g = acceleration due to gravity (approximately 9.8m/s2)
- Q = charge of the particle (given as 1.6×10−19C)
- e = electric field strength
Step 3: Calculate the Electric Field (E)
The electric field E between two plates is given by the formula:
E=Vd
Where:
- V = potential difference (3000 V)
- d = distance between the plates (5 cm = 0.05 m)
Substituting the values:
E=3000V0.05m=60000V/m
Step 4: Calculate the Electric Force (Qe)
The electric force F acting on the particle is given by:
F=Qe
Substituting the charge and electric field:
F=(1.6×10−19C)(60000V/m)
F=9.6×10−15N
Step 5: Substitute into the Equilibrium Equation
Now, substituting F into the equilibrium equation:
mg=9.6×10−15
m⋅9.8=9.6×10−15
Step 6: Solve for Mass (m)
Now, we can solve for m:
m=9.6×10−159.8
m≈9.8×10−16kg
Final Answer
The mass of the particle is approximately:
m≈9.8×10−16kg
---
The particle has a weight (mg) acting downwards and an electric force (Qe) acting upwards due to the electric field between the plates. Since the particle is in equilibrium, these two forces must balance each other.
Since the particle is in equilibrium:
mg=Qe
Where:
- m = mass of the particle
- g = acceleration due to gravity (approximately 9.8m/s2)
- Q = charge of the particle (given as 1.6×10−19C)
- e = electric field strength
The electric field E between two plates is given by the formula:
E=Vd
Where:
- V = potential difference (3000 V)
- d = distance between the plates (5 cm = 0.05 m)
E=3000V0.05m=60000V/m
The electric force F acting on the particle is given by:
F=Qe
Substituting the charge and electric field:
F=(1.6×10−19C)(60000V/m)
F=9.6×10−15N
Now, substituting F into the equilibrium equation:
mg=9.6×10−15
m⋅9.8=9.6×10−15
Now, we can solve for m:
m=9.6×10−159.8
m≈9.8×10−16kg
The mass of the particle is approximately:
m≈9.8×10−16kg
Similar Questions
A particle having a charge of 1.6x10−19C enters midway between the two plates of a parallel plate capacitor. The initial velocity of particle is parallel to the plates. A potential difference of300 Vis applied between the two plates. lfthe length of the plates is 10 cm and they are separated by 2 cm, calculate the greatest initial velocity for which the particle will not be able to come out of the plates. The mass of the particle is 12×10−24kg
[104m/s]
View SolutionAn electron is accelerated through a potential difference of 1000V and directed into space between two parallel plates separated by 2cm with a potential difference of 100V applied across them. If the electron enters perpendicular to the electric field between the polates, what magnetic field perpendicular to both the electron path and the electric field will be neccessary so that the electron may travel undeflected. Take e=1.6×10−19C and m=9×1031kg.
View Solution
Knowledge Check
A particle of mass 1.96×10−15 kg is kept in equilibrium between two horizontal metal plates having potential difference of 400 V separated apart by 0.02 m. then the charge on the particle is (e= electronic charge)
A3eB6eC2eD5eTwo metal pieces having a potential difference of 800V are 0.02m apart horizontally. A particle of mass 1.96×10−15kg is suspended in equilibrium between the plates. If the e is the elementary charge, then charge on the particle is
AeB3eC6eD8eA cathode ray tube contains a pair of parallel metal plates 1.0cm apart and 3.0cm long. A narrow horizontal beam of electron with a velocity of 3×107ms−1 is passed down the tube midway between the two plates. When a potential difference of 550V is maintained across the plates, it is found that the electron beam is so deflected that it just strikes the end of one of the plates. then the specific change of an electron (that is, the ratio of its charge to mass) in C/kg is :
A3.6×10−14C/kgB1.8×10−11C/kgC3.6×10−12C/kgD1.8×10−9C/kg
An oil drop with charge 1.6×10−18C is balanced in air between two metallic plates 10 mm apart. Calculate the voltage required between the plates if mass of the drop is 2.4×10−14kg.
View SolutionTwo particles, each having a mass of 5 g and charge. 1.0×10−7 C, stay in limiting wquilibrium on a horizontal. table with a seaprtion of 10 cm between them. The coefficient of friction beteen each partcle and the table. is the same. Find the value of this coefficient.
View SolutionA particle of mass 9×10−31 kg having a negative charge of 1.6×10−19C is projected horizontally with a velocity of 106ms−1 into a region between two infinite horizontal parallel plates of metal. The distance between the plates is d=0.3cm and the particle enters 0.1cm below the top plate, THe top and bottom plates are connected, respectively to the positive and negative terminal of a 30V battery. Find the components of hte velocity of hte paricle just before it hits one of the plates.
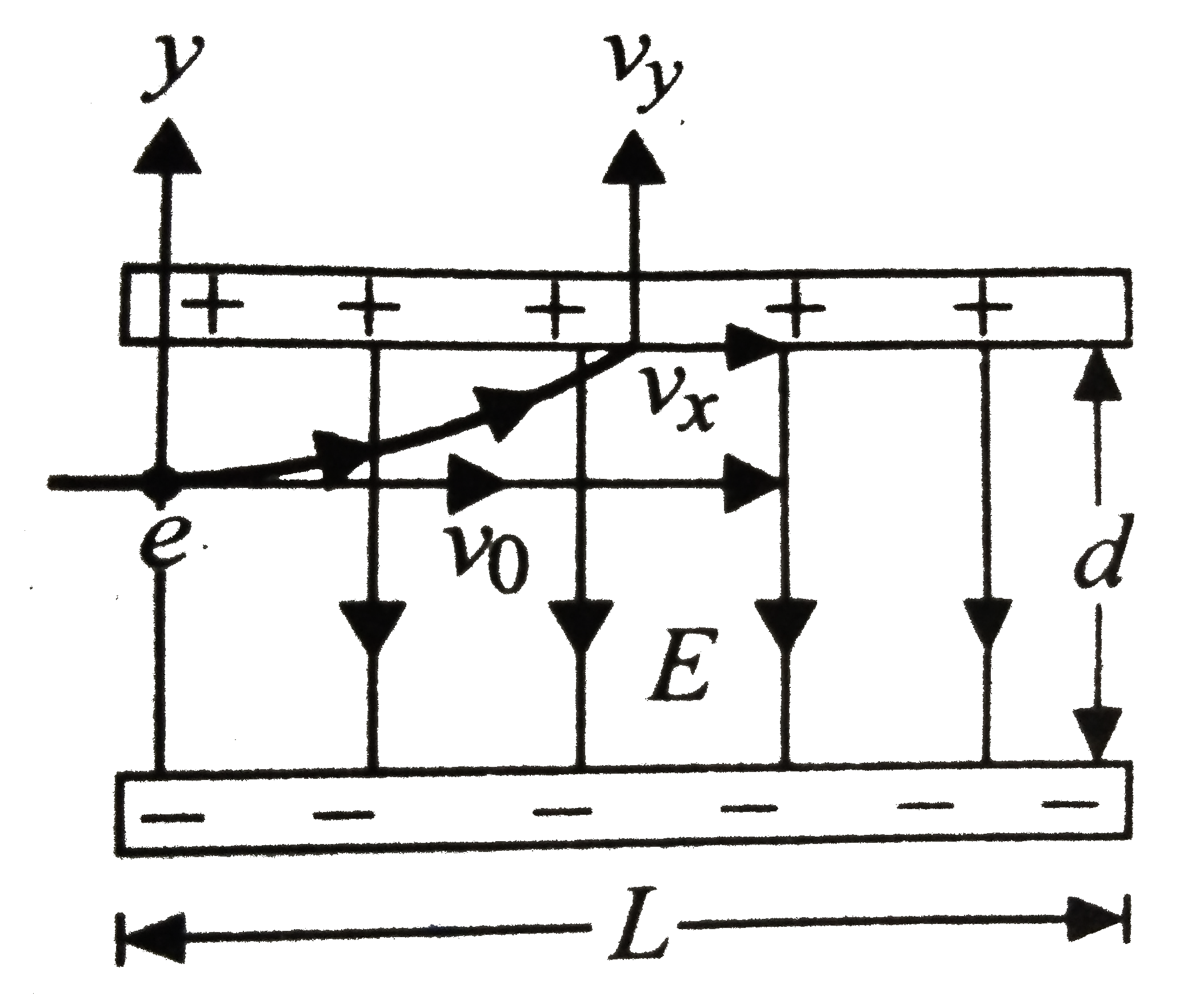
View SolutionA cathode ray tube contains a pair of parallel metal plates 1⋅0cm apart and 3⋅0cm long. A narrow horizontal beam of electrons with velocity of 3×107ms−1 is passed down the tube mid way between the two plates. When the potential difference of 550V is maintained across the plates, it is found that the electron beam is so deflected that it just strikes the end of one of the plates. Find the specific charge of an electron.
View SolutionAn ail drop having charge 2e is kept stationary between two parallel horizontal plates 2.0cm apart when a potential difference of 12000 volts is applied between them. If the density of oil is 900kg/m3, the radius of the drop will be
View Solution

