Four particles each having a charge q are placed on the four vertices of a regular pentagon. The distance of each comer from !be centre is 'a'. Find the electric field at the centre of pentagon.
We can calculate the electric field at centre by the superposition method i.e., by adding vectorially the electric field due to all the 4 charges at centre which will come out to be :
→Fcentre=−→F1+−→F2+−→F3+−→F4=Kqa2
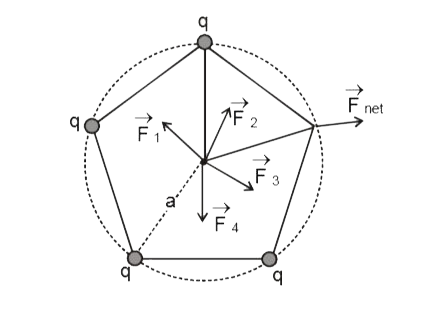
In the direction of the vector with no charge as shown in figure shown.
Alternate :
Consider pentagon with charges on all vector. Now, E.F. at centre must be zero due to symmetry

Thus E.F. due to 4 charge + E. F. due to 1 charge = 0 or E.F. due to 4 charges = –E.F . due to 1 charge Where – sign denotes that both the forces are in opposite direction.
Thus E.F. dut to 4 charges =–E.F. due to 1 charge
=Kqa2
[Another good example of superposition theorem]
Topper's Solved these Questions
- ELECTROSTATICS - I Book:MOTIONChapter:ELECTROSTATICS - I Exercise:EXERCISE - 1 (Section A)
Explore 10 Videos
- ELECTROSTATICS - I Book:MOTIONChapter:ELECTROSTATICS - I Exercise:EXERCISE - 1 (Section B)
Explore 10 Videos
- ELECTROSTATICSBook:MOTIONChapter:ELECTROSTATICSExercise:Exercise -3 Section (B) Previous Year Problems | JEE Main
Explore 30 Videos
- ELECTROSTATICS-IIBook:MOTIONChapter:ELECTROSTATICS-IIExercise:Exercise - 4 (Level - II)
Explore 30 Videos
Similar Questions
Knowledge Check
Find each interior of a regular pentagon.
A108∘B105∘C103∘D101∘Five point charges, +q each are placed at the five vertices of a regular hexagon. The distance of the center of the hexagon from any fo the vertices is a. the electric field at the center of the hexagon is
Aq4πε0a2Bq8πε0a2Cq16πε0a2DzeroFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
A14πε0qa2Bq16πε0a2C√2q4πε0a2D5q16πε0a2
Five charges, q each are placed at the corners of a regular pentagon of side a. (Refer the adjoining figure)
(a) (i) What will be the electric field at O, if the centre of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by -q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?

View SolutionFour identical point charges, each of charge q, are placed on the vertices of a regular hexagon of side a such that the net electric field at centre of hexagon is zero. If one of the charge is now removed, then the electric field at centre of hexagon is k- 4.60
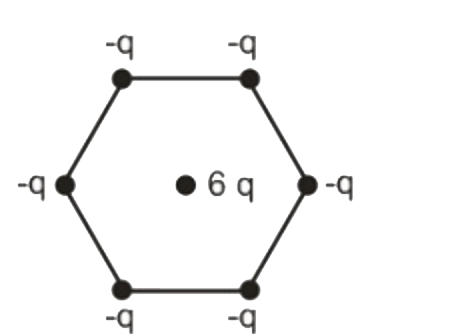
View SolutionSix negative equal charge are placed at the vertical of a regular hexagon . 6q charge is placed at the centre of the hexagon . Find the electric dipole moment of the system.
View SolutionSix point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
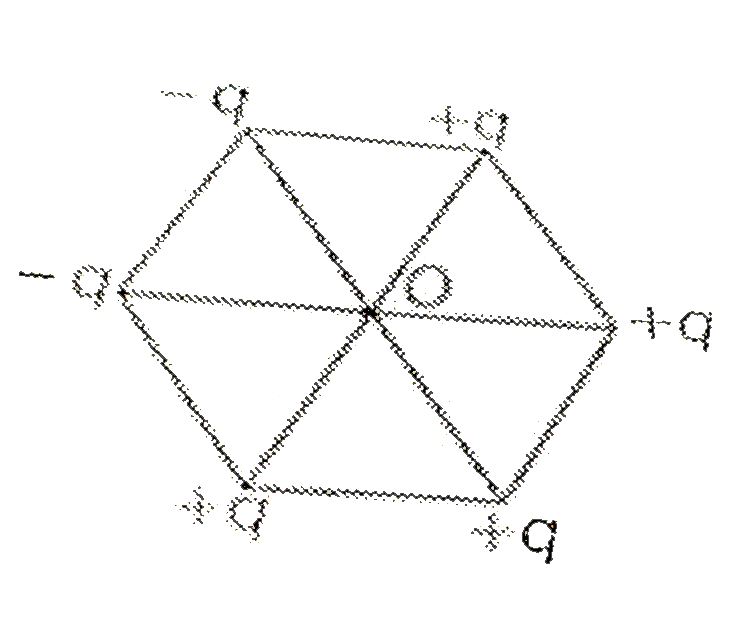
Find the magnitude of electric field at the centre of regular hexagon.
View SolutionFour point masses each of mass m are placed on vertices of a regular tetrahedron. Distance between any two masses is r.
View Solution