Four point masses each of mass m are placed on vertices of a regular tetrahedron. Distance between any two masses is r.
Gravitation field at centre at zero
Gravitation potential at centre is −4Gmr
Gravitation potential energy of system in −6Gm2r
Gravitation force on one of the point mass is √6Gm2r2
The correct Answer is:A, C, D
Eg=0 By symmetry
Potential energy of system =−6Gm2r
Force between two masses F=Gm2r2
Angle between any two force is 60∘
→F=→F1+→F2+→F3
F2net=F21+F22+F22+2→F1.→F2+2→F2.→F3+2→F3.→F1
F2net=3F2+3F2
Fnet=√6F
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.40
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.41
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.38
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Four point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
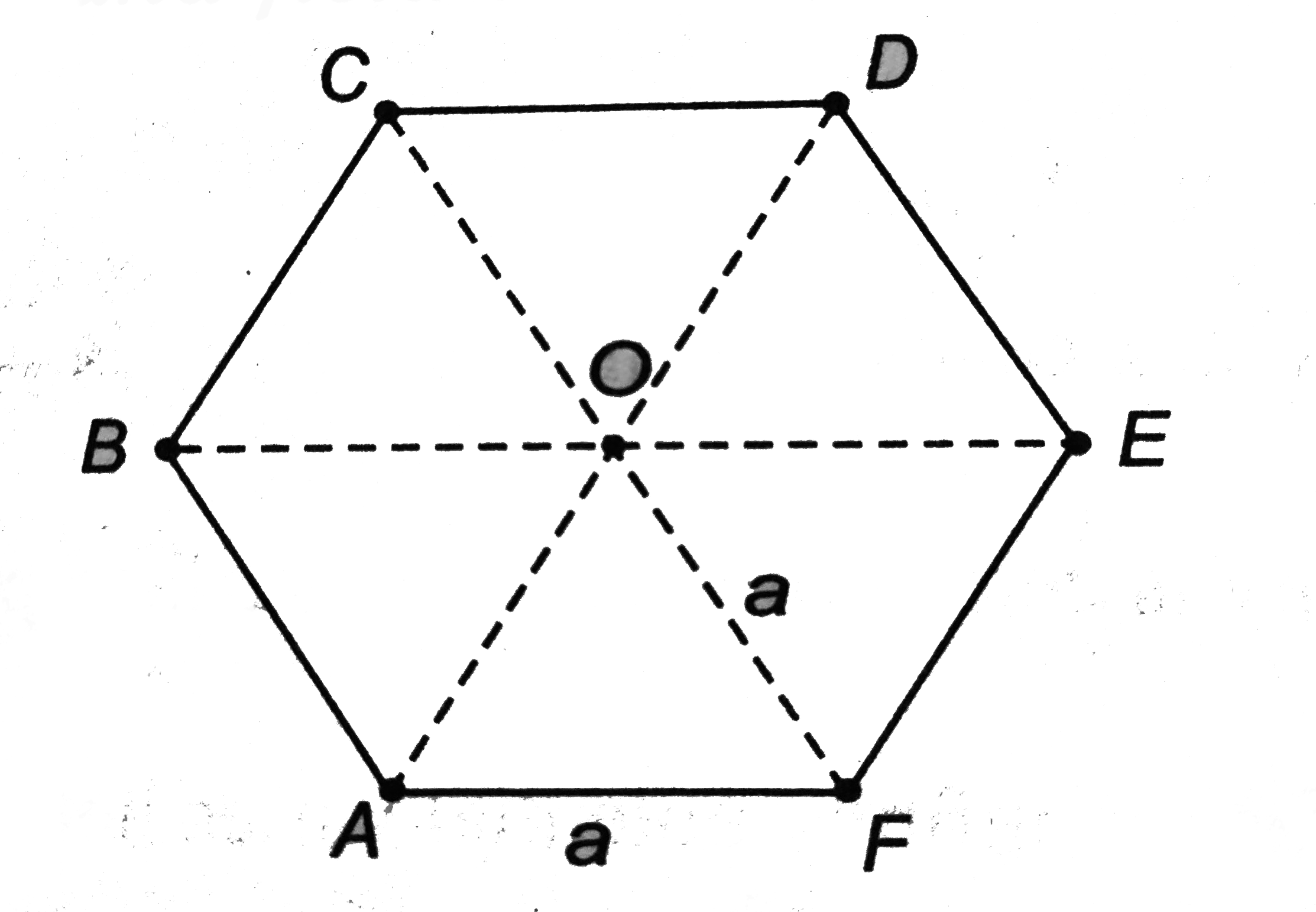 .
.
View SolutionFive point masses m each are kept at five vertices of a regular pentagon. Distance of centre of pentagon from any one of the verticle is 'a'. Find gravitational potential and filed strength at centre.
View Solution
Knowledge Check
Assertion : Four point masses each of mass m are placed at points 1, 2, 3 and 6 of a regular hexagon of side a. Then the gravitational field at the centre of hexagon is Gma2
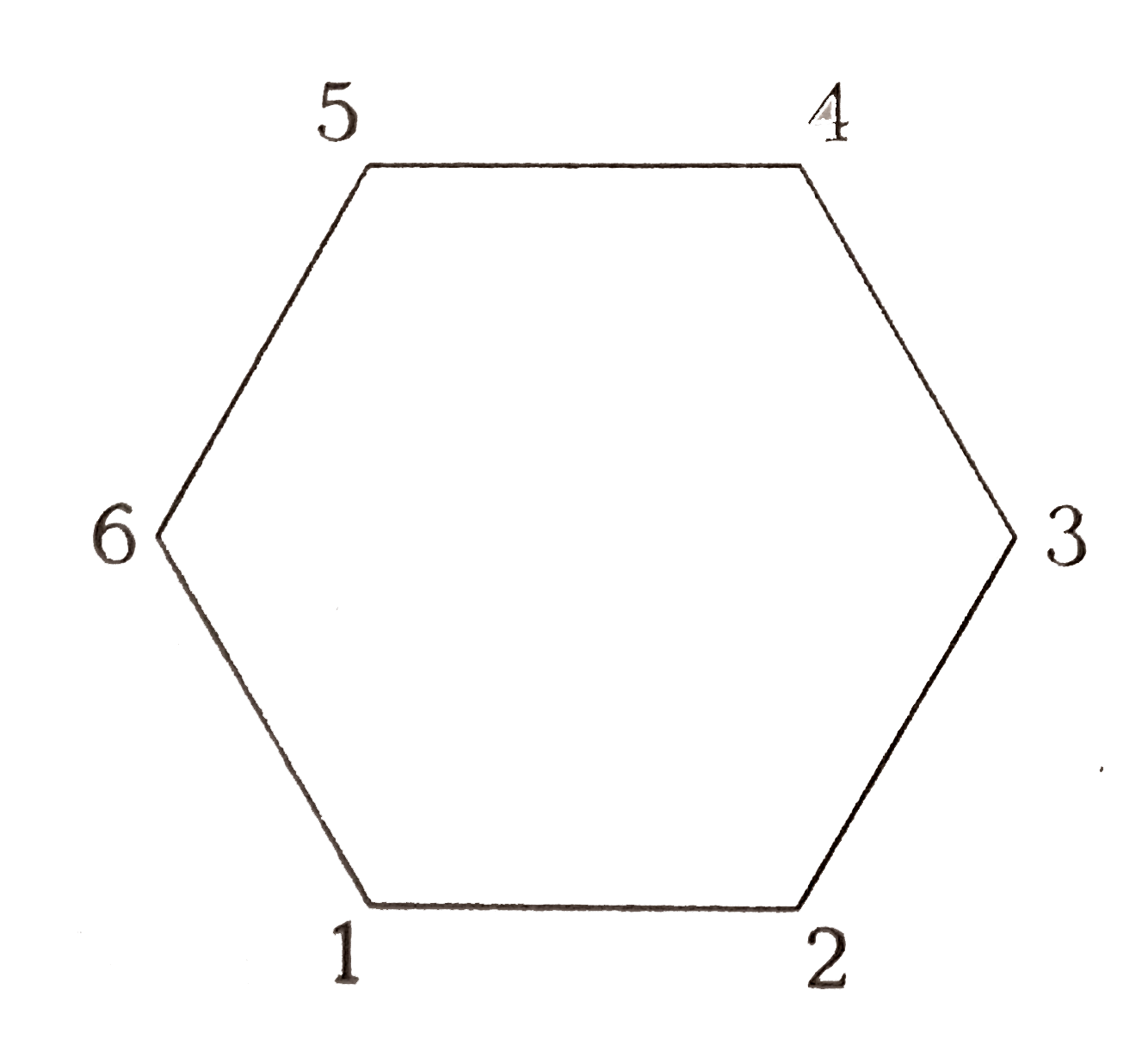
Reason : The field strength due to masses at 3 and 6 are cancelled out.AIf both Assertin and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are correct but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is falseDIf Assertion is false but Reason is trueFour particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−2√2GmlB−3√2GmlC−2GmlD−4√2Gml
(n−1) equal point masses each of mass m are placed at the vertices of a angular n-polygon. The vacent vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
View SolutionSix point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
View SolutionFour small point charges (each of equal magnitude q) are placed at four corners of a regular tetrahedron of side a. find out potential energy of charge system
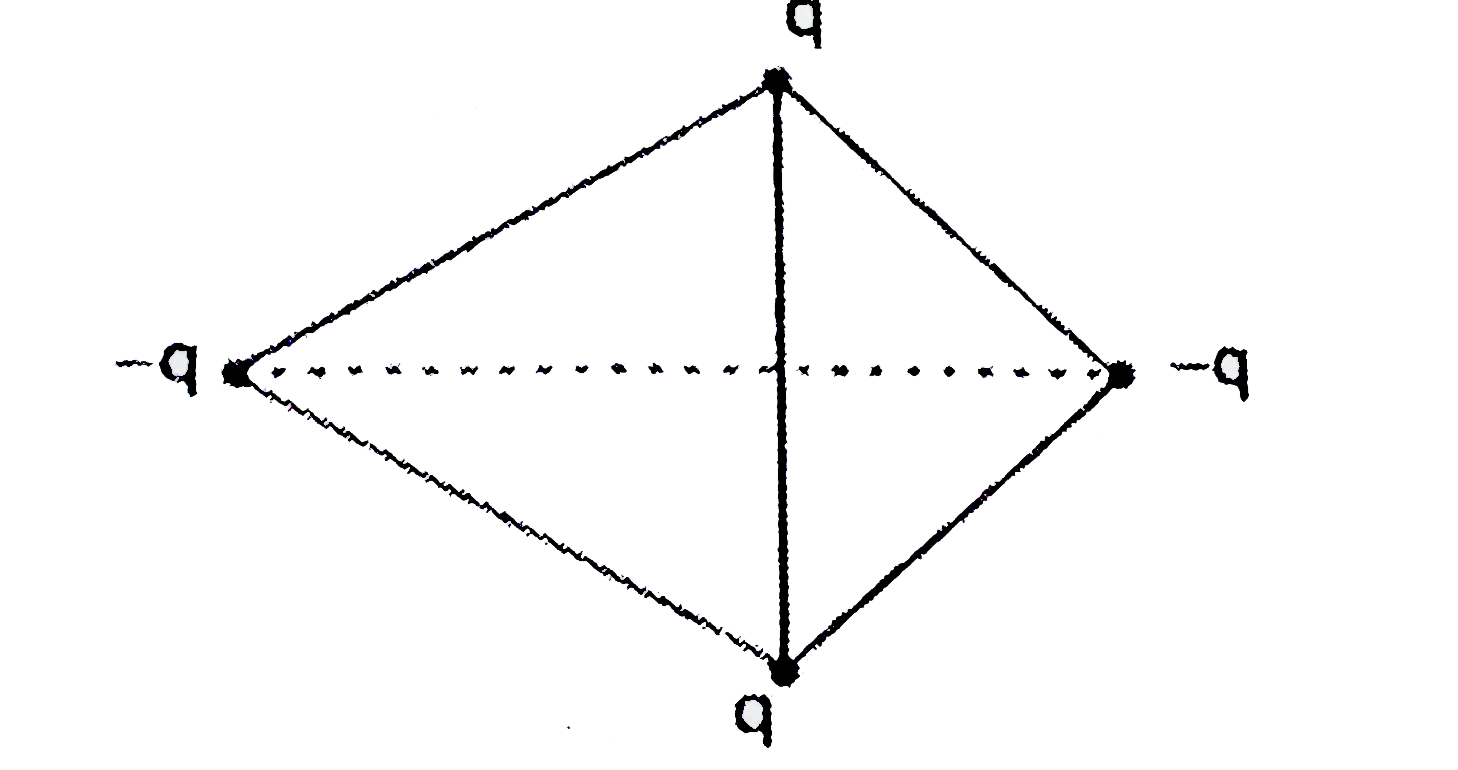
View SolutionFour masses (each of m) are placed at the vertices of a regular pyramid (triangular base) of side 'a'. Find the work done by the system while taking them apart so that they form the pyramid of side '2a'.
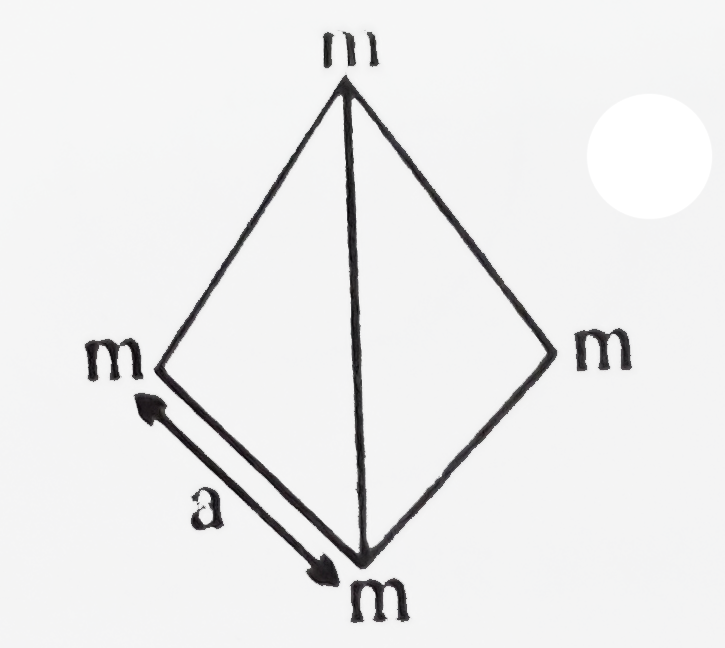
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?
View Solution
