A horizontal thin tube of length 2L completely filled with a liquid of density $δ$ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity $ω$ . Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The difference in the heights (h) of the liquid column in the two vertical thin tubes is :

A

$\frac{ω^{2} L^{2}}{2 g}$

B

$\frac{3 ω^{2} L^{2}}{2 g}$

C

$\frac{5 ω^{2} L^{2}}{2 g}$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

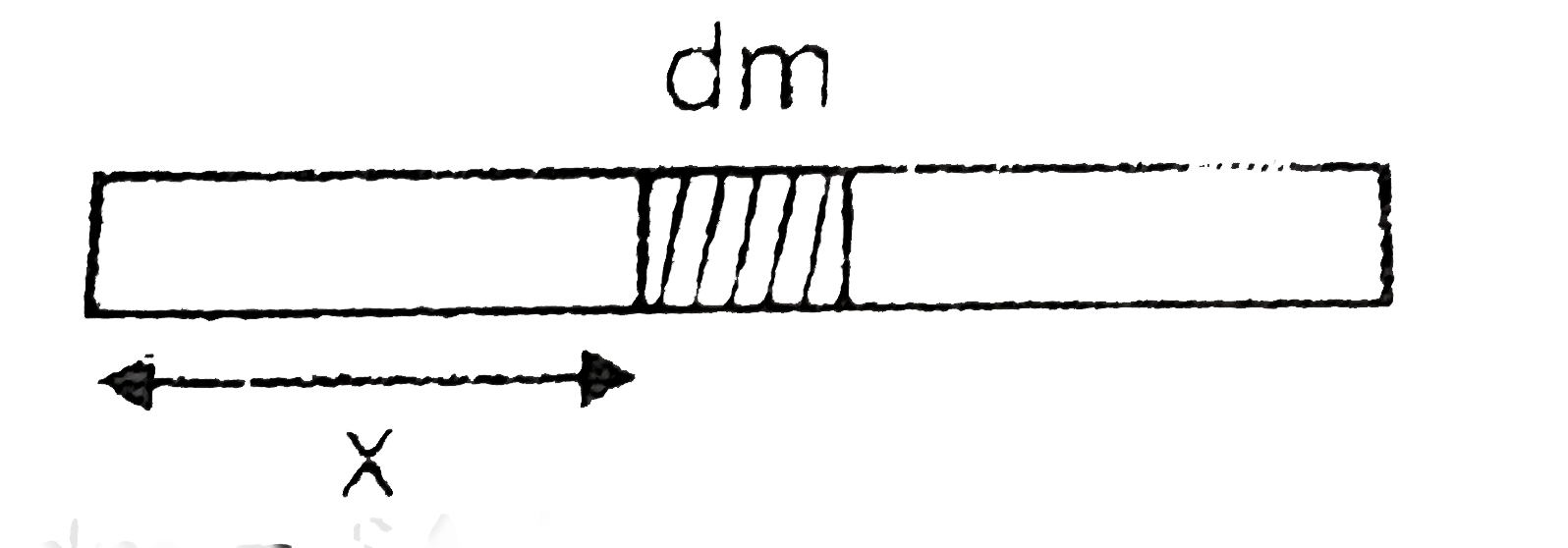
$d m = δ A d x$
$d P A = (δ A d x) a$
$\frac{d P}{d x} = δ ω^{3} x$
The difference in height
$h = y_{2} - y_{1} = \frac{ω^{2} {(2 L)}^{2}}{2 g} - \frac{ω^{2} L^{2}}{2 g} = \frac{3 ω^{2} L^{2}}{2 g}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A horizontal thin tube of length 2L completely filled with a liquid of density $δ$ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity $ω$ . Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The graph of the pressure gradient $(\frac{d P}{d x})$ with the distance x meaured from the axis of rotation is :
A
B
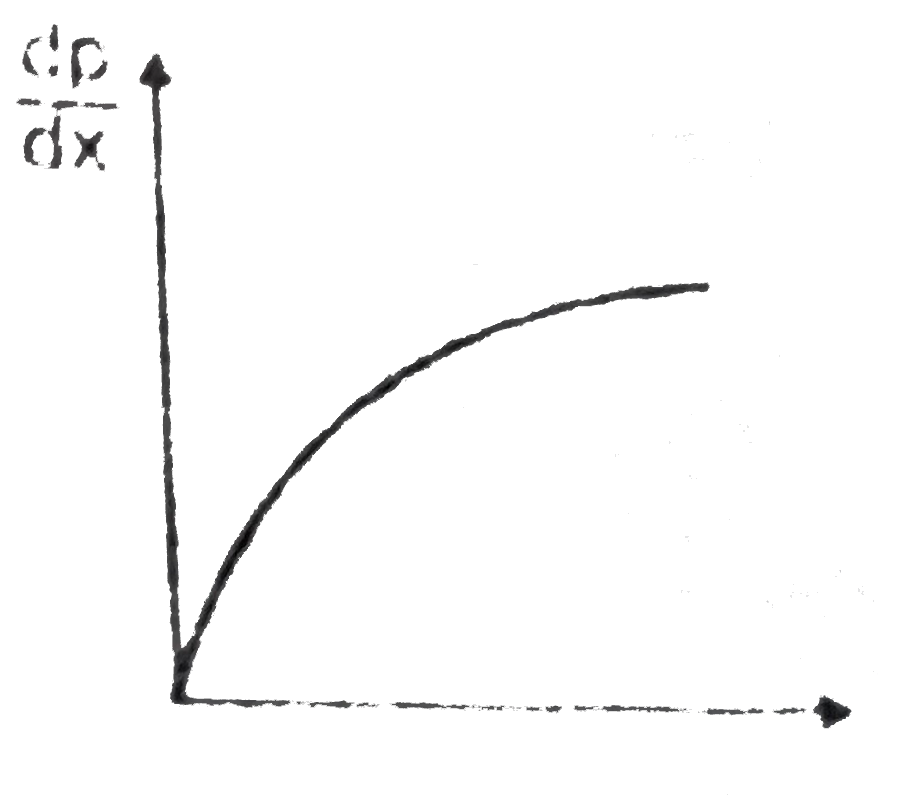C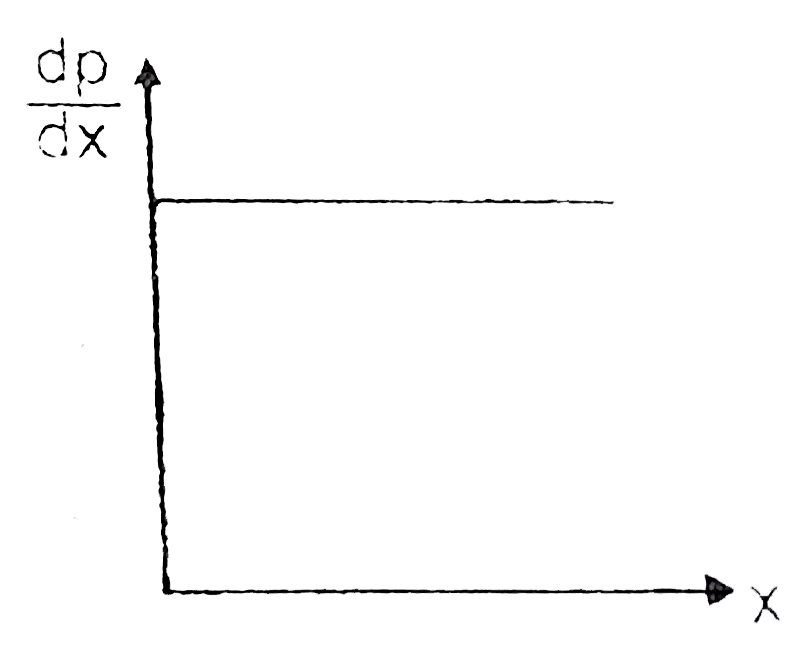
DNone of these
Question 2 - Select One
If a horizontal cylindrical tube, partly filled with water is rapidly rotated about a vertical axis passing through its centre, the moment of inertia of the water about its axis will
Adecrease
Bincrease
Cnot change
Dincrease or decrease depending upon clockwise or anticlockwise sense of rotation
Question 3 - Select One or More
Water is flowign is streamline motion through a tube with its axis horizontal. Consider two points A and B in the tube at the same horizontal level
AThe pressures at A and B are equal for any shape of the tube
Bthe pressure are never equal
Cthe pressure are equal even if the tube has a uniform cross section
Dthe pressures may be equal even if the tube has a nonuniform cross section.

RESONANCE-DAILY PRACTICE PROBLEM-DPP No.39

Home
Ask Doubt
Profile