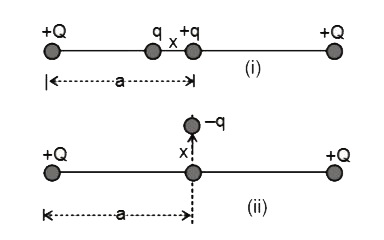
Two small particles charged with equal positive charges Q each, are fixed apart at a distance 2a. Another small particle having a charge q lies midway between the fixed charges. Show that
(i) For small displacement (relative to a) along line joining the fixed charges, the middle charge executes SHM'if it is +ve and
(ii) For small lateral displacement, it executes SHM ifit is-ve. Compare the frequencies of oscillation in the two cases
The two situations are shown in figure (i) Let x be the displacement of the charge +q from the mean position. Now net force acting on the charge q toward its equilirbium position is
F=KQq(a−x)2−KQq(a+x)2
=4KQqax(a2−x2)2≈4KQqaxa4[Asx<<a]
≈4KQqxa3
Restoring acceleration, a =Fm=−4KQqxma3
[– ve sign shows restoring tendency]
a=−ω2x [where m is the mass of the charge] As acceleration is directly proportional to displacement, hence the motion is SHM. Its time period T1 is given by
T1=2πω
T1=2π√(ma34QqK)=2π√πε0ma3qQ ...(1)
(ii) Restoring force on –q toward Q is given by
F=2KQq(a2+x2).x√(a2+x2)
=2KQq(a2+x2)3/2≈2KQqxa3 [As x <<a]
Restoring acceleration =Fm=−2KQqma3x
a=−ω2x
Hence the motion is SHM. Its time period T2 is given by
T2=2πω
T2=2π√ma32QqK=2π√2πε0ma3qQ ...(2)
Now, n1n2=T2T1=√2
Topper's Solved these Questions
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section A)
10 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 1 (Section B)
10 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (B) Previous Year Problems | JEE Main
30 Videos
- ELECTROSTATICS-IIBOOK - MOTIONCHAPTER - ELECTROSTATICS-IIEXERCISE - Exercise - 4 (Level - II)
30 Videos
Similar Questions
Knowledge Check
Two charges of equal magnitude q are placed at a distance 2a Another charge q of mass m, is placed midway between the two charges on X-axis. If this charges is displaced from equilibruim state to a distance x(x<<a), then the particle :-
Awill execute simple harmonic motion about equilibrium positionBwill be oscillating about equilibrium poition but will nit execute simple harmonic motionCwill not return back to the equilibrium positionDwill stop at equilibrium positionTwo equal charges q are kept fixed at −aand+a along the x-axis. A particle of mass m and charge q2 is brought to the origin and given a small displacement along the x-axis, then
Athe particle executes oscillatory motionBthe particle remains stationaryCthe particle executes SHM along x-axisDthe particle executes SHM along y-axisTwo equal charges q are kept fixed at a and +a along the x-axis. A particle of mass m and charge q2 is brought to the origin and given a small displacement along the x-axis then
Athe particle executes oscillartory motionBthe particle remains stationaryCthe partiel executes, SHM along x-axisDthe particle executes SHM along y-axis
A charged particle of mass m having charge q remains in equilibrium at height d above a fixed charge Q. Now the charged particle is slightly displaced along the line joining the charges, show that it will executes S.H.M. and find the time period of oscillation.
View SolutionTwo points charges , each Q , are fixed at separation 2d. A charged particle having charge q and mass m is placed between them.
(a) Now this charged particle is slightly displaced along the line joining the charges , slow that it will execute simple harmonic motion and find the time period of oscillation.
(b) If charge q is negative and it is displaced slightly perpendicular to the line joining the charges , repeat the part (a).
View SolutionA pair of equal and opposite point charge "+q" and "-q separated by small distance "2a is called
View SolutionTwo charges, each equal to q, are kept at x=−a and x=a on the x-axis. A particle of mass m and charge q0=q2 is placed at the origin. If charge q0 is given a small displacement (y<<a) along the y-axis, the net force acting on the particle is proportional to
View SolutionTwo equal charges of magnitude Q each are placed at a distance d apart. Their electrostatic energy is E. A third charge −Q/2 is brought midway between these two charges. The electrostatic energy of the system is now
View Solution
