A thin rod AB of length a has variable mass per unit length ρ0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Find moment of inertia of the rod about an axis passing through A and perpendicular to AB.
The correct Answer is:7a3ρ012
Step by step video, text & image solution for A thin rod AB of length a has variable mass per unit length rho_(0) (1 + (x)/(a)) where x is the distance measured from A and rho_(0) is a constant. Find moment of inertia of the rod about an axis passing through A and perpendicular to AB. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Exercise - 4 (Level - I)
Explore 24 Videos
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Exercise - 4 (Level - II)
Explore 49 Videos
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Exercise - 3 (Level - I)
Explore 27 Videos
- ALTERNATING CURRENTBook:MOTIONChapter:ALTERNATING CURRENTExercise:EXERCISE - 4 (LEVEL - II)
Explore 14 Videos
Similar Questions
A thin rod AB of length a has variable mass per unit length ρ0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Find the mass M of the rod.
View SolutionA thin rod AB of length a has variable mass per unit length P0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Find the position of centre of mass of the rod.
View Solution
Knowledge Check
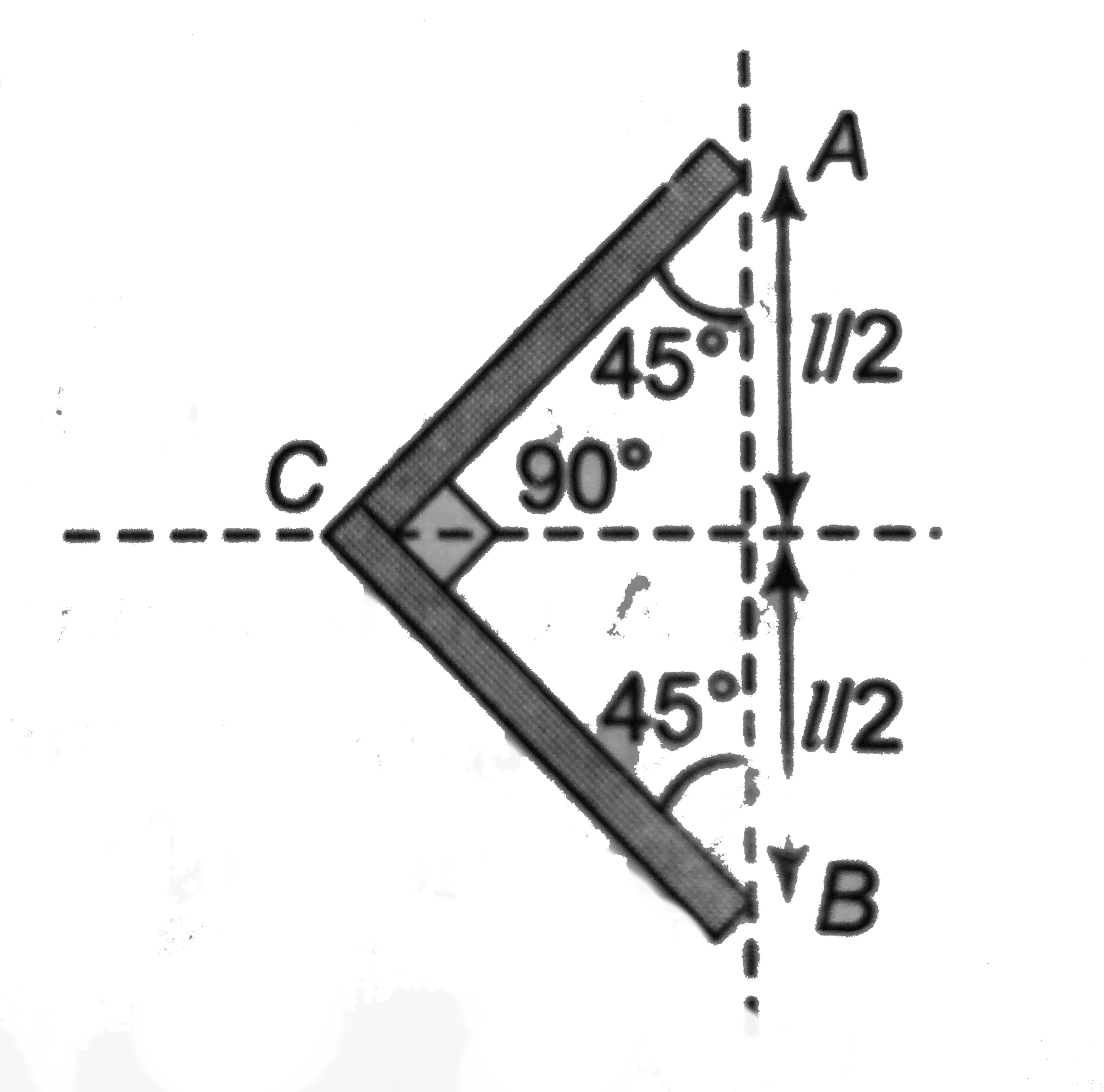
Linear mass density of the two rods system, AC and CD is x. moment of inertia of two rods about an axis passing through AB isAxl34√3Bxl3√2Cxl34Dxl36√2A thin rod of length l and mass m is turned at mid-point O at angle of 60°. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
 Aml2/3Bml26Cml28Dml212
Aml2/3Bml26Cml28Dml212A rod of length 2 m, has a mass of 0.12 kg. Its moment of inertia about an axis passing through its one end and perpendicular to the length of the rod is
A0.16 kg - m2B0.12 kg - m2C0.32 kg - m2D0.08 kg - m2
A thin rod AB of length a has variable mass per unit length ρ0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Find minimum value of impulse P if B passes through a point vertically above A.
View SolutionA thin rod AB of length a has variable mass per unit length ρ0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Rod is freely pivoted at A and is hanging in equilibrium when it is struck by a horizontal impulse of magnitude P at the point B. Find the angular velocity with which the rod begins to rotate.
View SolutionThe linear mass density of a thin rod AB of length L varies from A to B as λ(x)=λ0(1+xL). Where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicualr to the rod is :
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.

View SolutionA 1m long rod has a mass of 0.12 kg. The moment of inertia about an axis passin through the centre and perpendicular to the length of rod will be
View Solution

